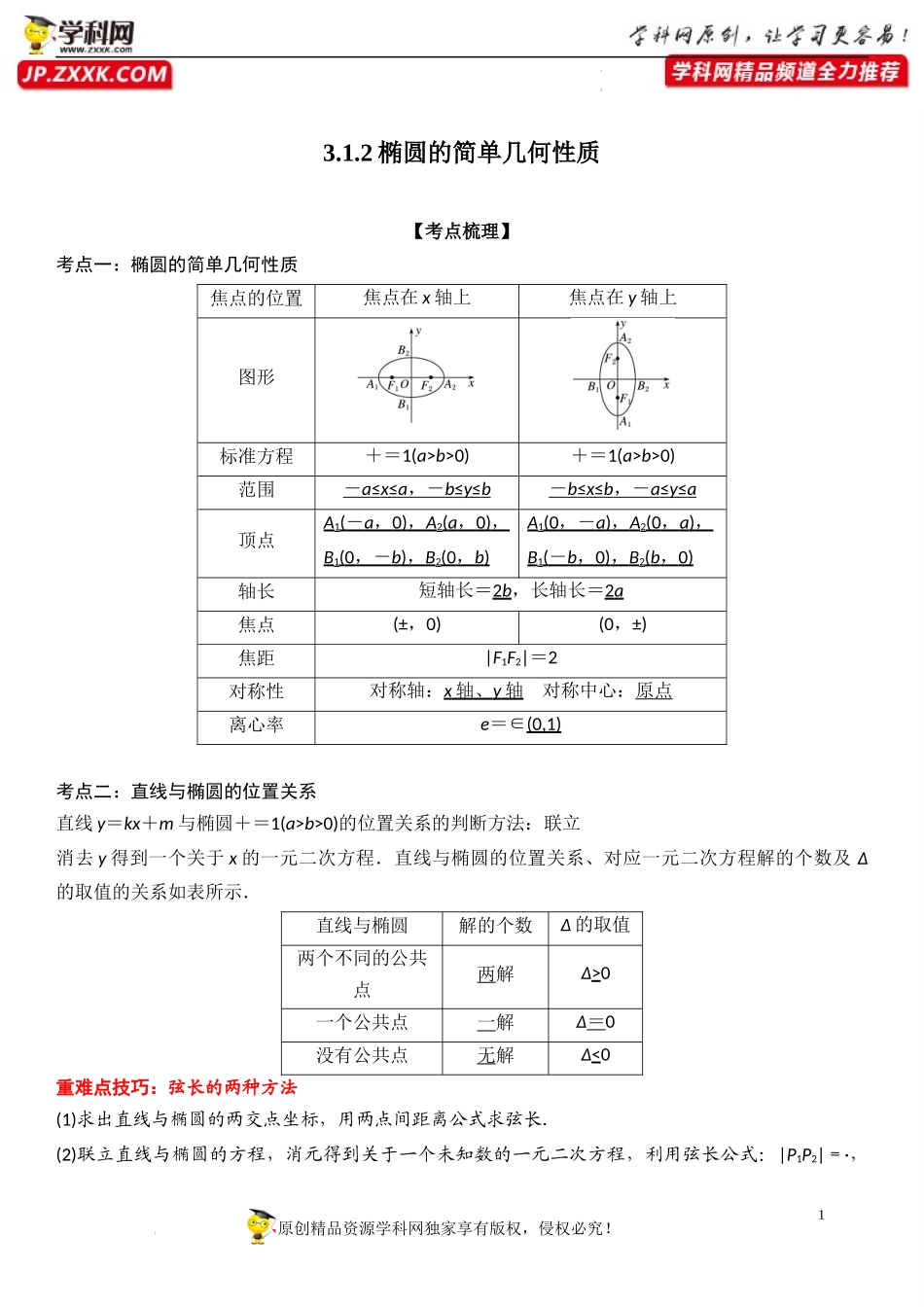
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司3.1.2椭圆的简单几何性质【考点梳理】考点一:椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程+=1(a>b>0)+=1(a>b>0)范围-a≤x≤a,-b≤y≤b-b≤x≤b,-a≤y≤a顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)轴长短轴长=2b,长轴长=2a焦点(±,0)(0,±)焦距|F1F2|=2对称性对称轴:x轴、y轴对称中心:原点离心率e=∈(0,1)考点二:直线与椭圆的位置关系直线y=kx+m与椭圆+=1(a>b>0)的位置关系的判断方法:联立消去y得到一个关于x的一元二次方程.直线与椭圆的位置关系、对应一元二次方程解的个数及Δ的取值的关系如表所示.直线与椭圆解的个数Δ的取值两个不同的公共点两解Δ>0一个公共点一解Δ=0没有公共点无解Δ<0重难点技巧:弦长的两种方法(1)求出直线与椭圆的两交点坐标,用两点间距离公式求弦长.(2)联立直线与椭圆的方程,消元得到关于一个未知数的一元二次方程,利用弦长公式:|P1P2|=·,2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司其中x1,x2(y1,y2)是上述一元二次方程的两根,由根与系数的关系求出两根之和与两根之积后代入公式可求得弦长.【题型归纳】题型一:椭圆的焦点、焦距.顶点,长短轴1.(2022·山东滨州·高二期末)已知椭圆与椭圆,则下列结论正确的是()A.长轴长相等B.短轴长相等C.焦距相等D.离心率相等2.(2021·山东济宁·高二期中)椭圆与椭圆的()A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等3.(2021·河南·襄城县实验高级中学高二阶段练习(文))已知椭圆的左右焦点分别是、,,过的直线与椭圆C交于A,B两点,则的面积是()A.B.C.D.题型二:椭圆的椭圆的范围问题4.(2022·江苏·高二)已知椭圆的焦距为4,则有()A.椭圆C的焦点在x轴上B.椭圆C的长轴长为6C.椭圆C的离心率为D.以椭圆C的四个顶点为顶点的四边形的周长为3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司5.(2021·江苏·高二单元测试)在椭圆上有两个动点,为定点,,则的最小值为()A.B.C.D.16.(2022·福建省永春美岭中学高二期中)已知点、,动点满足:直线的斜率与直线的斜率之积为,则的取值范围为()A.B.C.D...