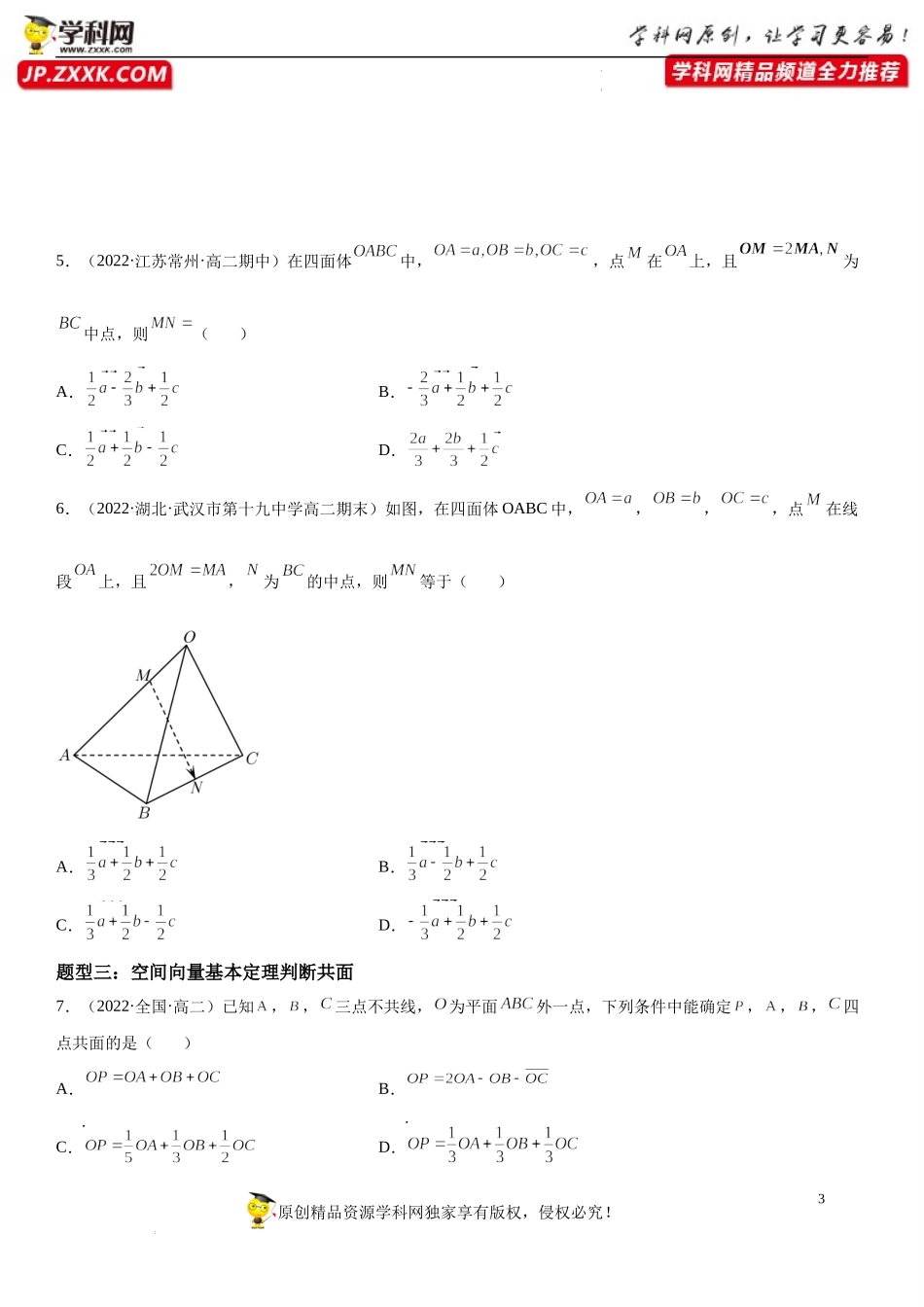
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司1.2空间向量基本定理【考点梳理】考点一空间向量基本定理如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得p=xa+yb+zc.我们把{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量.考点二空间向量的正交分解1.单位正交基底如果空间的一个基底中的三个基向量两两垂直,且长度都是1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.2.向量的正交分解由空间向量基本定理可知,对空间任一向量a,均可以分解为三个向量xi,yj,zk使得a=xi+yj+zk.像这样把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.考点三证明平行、共线、共面问题(1)对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.(2)如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p=xa+yb.考点三求夹角、证明垂直问题(1)θ为a,b的夹角,则cosθ=.(2)若a,b是非零向量,则a⊥b⇔a·b=0.知识点三求距离(长度)问题=(=).【题型归纳】2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司题型一:空间向量基底概念1.(2021·广东·广州市海珠中学高二期中)下列说法正确的是()A.任何三个不共线的向量可构成空间向量的一个基底B.空间的基底有且仅有一个C.两两垂直的三个非零向量可构成空间的一个基底D.直线的方向向量有且仅有一个2.(2021·云南师大附中高二期中)已知能构成空间的一个基底,则下面的各组向量中,不能构成空间基底的是()A.B.C.D.3.(2021·湖南·周南中学高二)设向量不共面,则下列可作为空间的一个基底的是()A.B.C.D.题型二:空间基底表示向量4.(2022·四川·成都外国语学校高二阶段练习(理))如图,在三棱锥中,设,若,则=()A.B.C.D.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司5.(2022·江苏常州·高二期中)在四面体中,,点在上,且为中点,则()A.B.C.D.6.(2022·湖北·武汉市第十九中学高二期末)如图,在四面体OABC中,,,,点在线段上,且,为的中点,则等于()A.B.C.D.题型三:空间向量基本定理判断共面7.(2022·全国·高二)已知,,三点不共线,为平面...