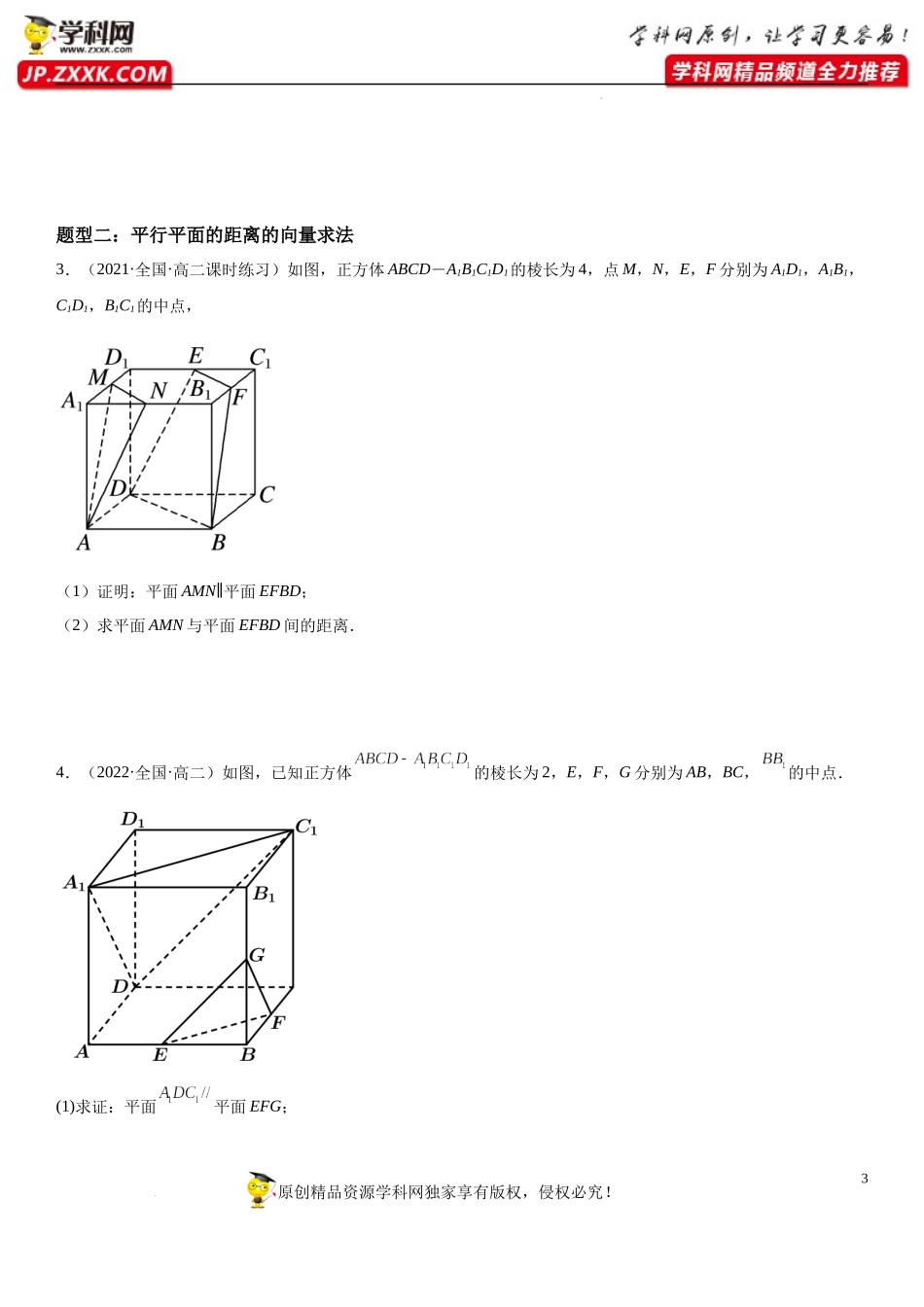
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司1.4.2用空间向量研究距离、夹角问题【考点梳理】考点一:空间向量中的距离问题1.点P到直线l的距离已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点,设向量AP在直线l上的投影向量为AQ=a,则点P到直线l的距离为2.点P到平面α的距离设平面α的法向量为n,A是平面α内的定点,P是平面α外一点,则点P到平面α的距离为.考点二:空间向量中的夹角问题角的分类向量求法范围两条异面直线所成的角设两异面直线l1,l2所成的角为θ,其方向向量分别为u,v,则cosθ=|cos〈u,v〉|=直线与平面所成的角设直线AB与平面α所成的角为θ,直线AB的方向向量为u,平面α的法向量为n,则sinθ=|cos〈u,n〉|=两个平面的夹角设平面α与平面β的夹角为θ,平面α,β的法向量分别为n1,n2,则cosθ=|cos〈n1,n2〉|=【题型归纳】题型一:点到平面的距离的向量求法2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司1.(2022·浙江省淳安中学高二期中)如图,已知三棱锥,平面,,,,.、分别为、的中点.(1)证明:平面;(2)求点到平面的距离.2.(2022·江苏常州·高二期中)如图,底面为正方形的平行六面体的各个棱的长度均为,平面平面分别是的中点.(1)证明:平面;(2)求点C到面的距离.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司题型二:平行平面的距离的向量求法3.(2021·全国·高二课时练习)如图,正方体ABCD-A1B1C1D1的棱长为4,点M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,(1)证明:平面AMN∥平面EFBD;(2)求平面AMN与平面EFBD间的距离.4.(2022·全国·高二)如图,已知正方体的棱长为2,E,F,G分别为AB,BC,的中点.(1)求证:平面平面EFG;4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司(2)求平面与平面EFG间的距离.题型三:异面直线夹角的向量求法5.(2022·江苏·涟水县第一中学高二阶段练习)如图所示,在四棱维中,面,且PA=AB=BC==2.(1)求与所成的角;(2)求直线与面所成的角的余弦值.6.(2022·江西南昌·高二期中(理))三棱锥中,,平面平面ABC,,,E,F分別为PC和PB的中点,平面平面.(1)证明:直线;(2)设M是直线l上一点,且直线PB与平面AEF所成的角为,直线PM与直线EF所成的角为,满足,5原创精品资源学科网独家享有版权,侵权必究!学科网(北京...