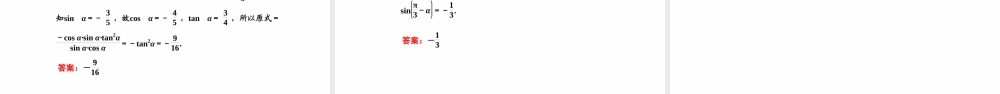【精品课件】第02讲 同角三角函数的基本关系与诱导公式-备战2022年高考数学一轮复习精品课件（新高考地区专用）.pptxVIP免费

数学第2讲同角三角函数的基本关系与诱导公式高三一轮复习重难点题型考点一同角三角函数基本关系式的应用考向(一)“知一求二”问题[例1]已知x∈π2，π，tanx＝－43，则cos－x－π2等于()A．35B．－35C．－45D．45[解析] tanx＝sinxcosx＝－43，∴cosx＝－34sinx，∴sin2x＋cos2x＝sin2x＋916sin2x＝2516sin2x＝1，∴sin2x＝1625．又x∈π2，π，∴sinx＝45，∴cos－x－π2＝cosπ2＋x＝－sinx＝－45．[答案]C考向(二)sinα，cosα的齐次式问题[例2]已知tanαtanα－1＝－1，求下列各式的值：(1)sinα－3cosαsinα＋cosα；(2)sin2α＋sinαcosα＋2．[解]由已知得tanα＝12．(1)sinα－3cosαsinα＋cosα＝tanα－3tanα＋1＝－53．(2)sin2α＋sinαcosα＋2＝sin2α＋sinαcosαsin2α＋cos2α＋2＝tan2α＋tanαtan2α＋1＋2＝122＋12122＋1＋2＝135．考向(三)“sinα±cosα，sinαcosα”之间的关系的应用[例3]已知x∈(－π，0)，sinx＋cosx＝15．(1)求sinx－cosx的值；(2)求sin2x＋2sin2x1－tanx的值．[解](1)由sinx＋cosx＝15，平方得sin2x＋2sinxcosx＋cos2x＝125，整理得2sinxcosx＝－2425．∴(sinx－cosx)2＝1－2sinxcosx＝4925．由x∈(－π，0)，知sinx<0，又sinx＋cosx>0，∴cosx>0，则sinx－cosx<0，故sinx－cosx＝－75．(2)sin2x＋2sin2x1－tanx＝2sinxcosx＋sinx1－sinxcosx＝2sinxcosxcosx＋sinxcosx－sinx＝－2425×1575＝－24175．利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．1．(2020·河南六市一模)已知cosπ2＋α＝35，且α∈π2，3π2，则tanα＝()A．43B．34C．－34D．±34√解析：因为cosπ2＋α＝35，所以sinα＝－35.又α∈π2，3π2，所以cosα＝－1－sin2α＝－45，所以tanα＝sinαcosα＝34.2．已知tanα＝－34，则sinα(sinα－cosα)＝()A.2125B.2521C.45D.54√解析：sinα(sinα－cosα)＝sin2α－sinαcosα＝sin2α－sinαcosαsin2α＋cos2α＝tan2α－tanαtan2α＋1，将tanα＝－34代入得原式＝－342－...