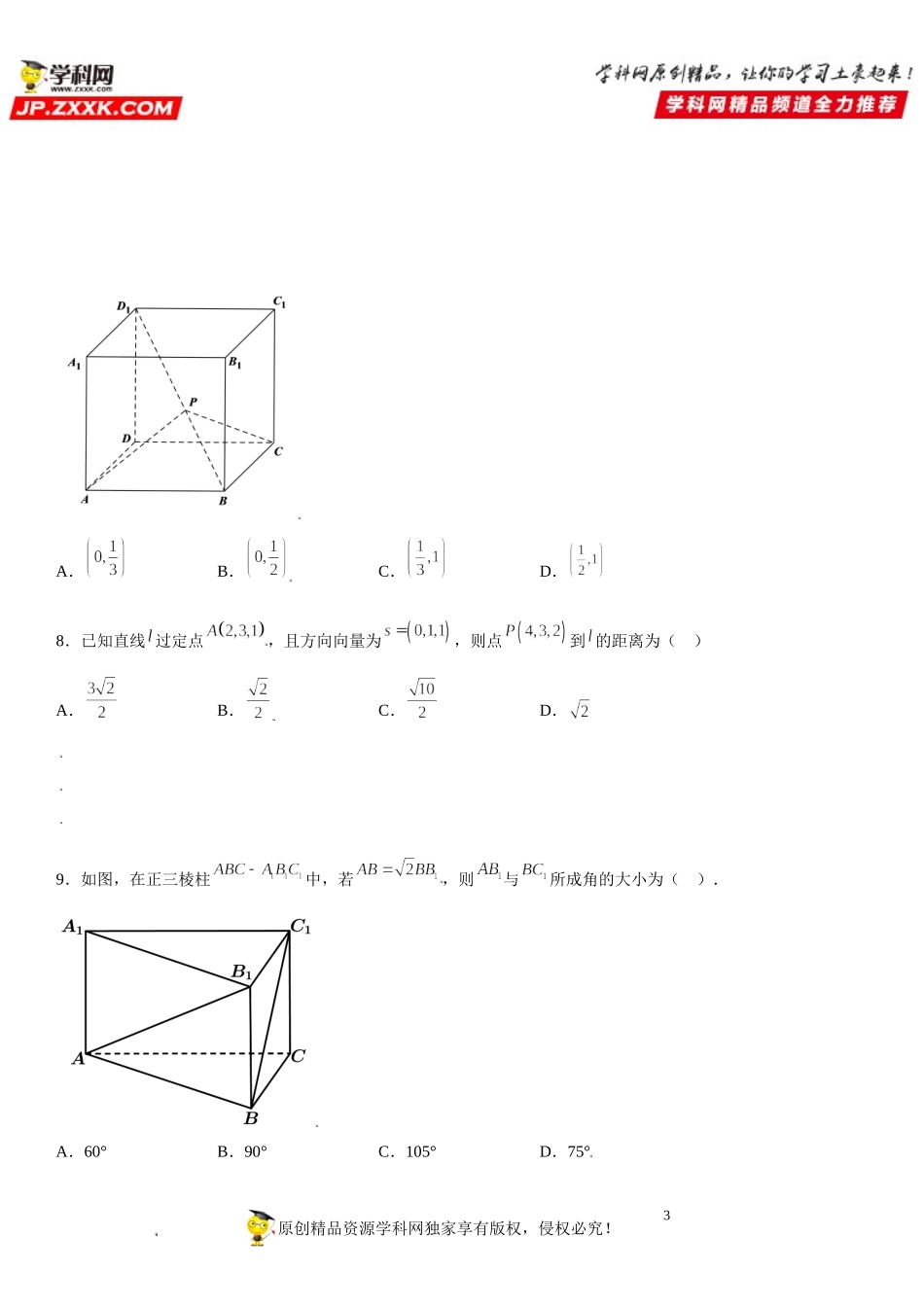
1高二数学《考点•题型•技巧》精讲与精练高分突破系列(人教A版选择性必修第一册)专题强化训练一:空间向量的在立体几何中的应用一、单选题1.在长方体中,,,则异面直线与所成角的余弦值为()A.B.C.D.2.已知、、分别是正方形边、及对角线的中点,将三角形沿着进行翻折构成三棱锥,则在翻折过程中,直线与平面所成角的余弦值的取值范围为()A.B.C.D.3.长方体,,,点在长方体的侧面上运动,,则二面角的平面角正切值的取值范围是()A.B.C.D.4.如图,在圆锥中,,为底面圆的两条直径,,且,,,异面直线与所成角的正切值为()原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司2A.B.C.D.5.在如图所示的四棱锥中,,,,,,且,则直线与平面所成角的正弦值为()A.B.C.D.6.已知二面角的大小为,和是两条异面直线,且,则与所成的角的大小为()A.B.C.D.7.已知动点P在正方体的对角线(不含端点)上.设,若为钝角,则实数的取值范围为()原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司3A.B.C.D.8.已知直线过定点,且方向向量为,则点到的距离为()A.B.C.D.9.如图,在正三棱柱中,若,则与所成角的大小为().A.60°B.90°C.105°D.75°原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司410.直三棱柱中,若,,是中点,过作这个三棱柱的截面,当截面与平面所成的锐二面角最小时,这个截面的面积为()A.2B.C.D.二、多选题11.下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是()A.两条不重合直线,的方向向量分别是,,则B.两个不同的平面,的法向量分别是,,则C.直线的方向向量,平面的法向量是,则D.直线的方向向量,平面的法向量是,则12.已知,分别是正方体的棱和的中点,则()原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司5A.与是异面直线B.与所成角的大小为C.与平面所成角的余弦值为D.二面角的余弦值为13.在四棱锥中,底面为平行四边形,底面,则下列结论正确的是()A.B.与平面所成的角为C.异面直线与所成角的余弦值为D.二面角的余弦值为14.在棱长为a的正方体中,分别是的中点下列说法正确的是()原创精品资源学科网独家享有版权,侵权必究...