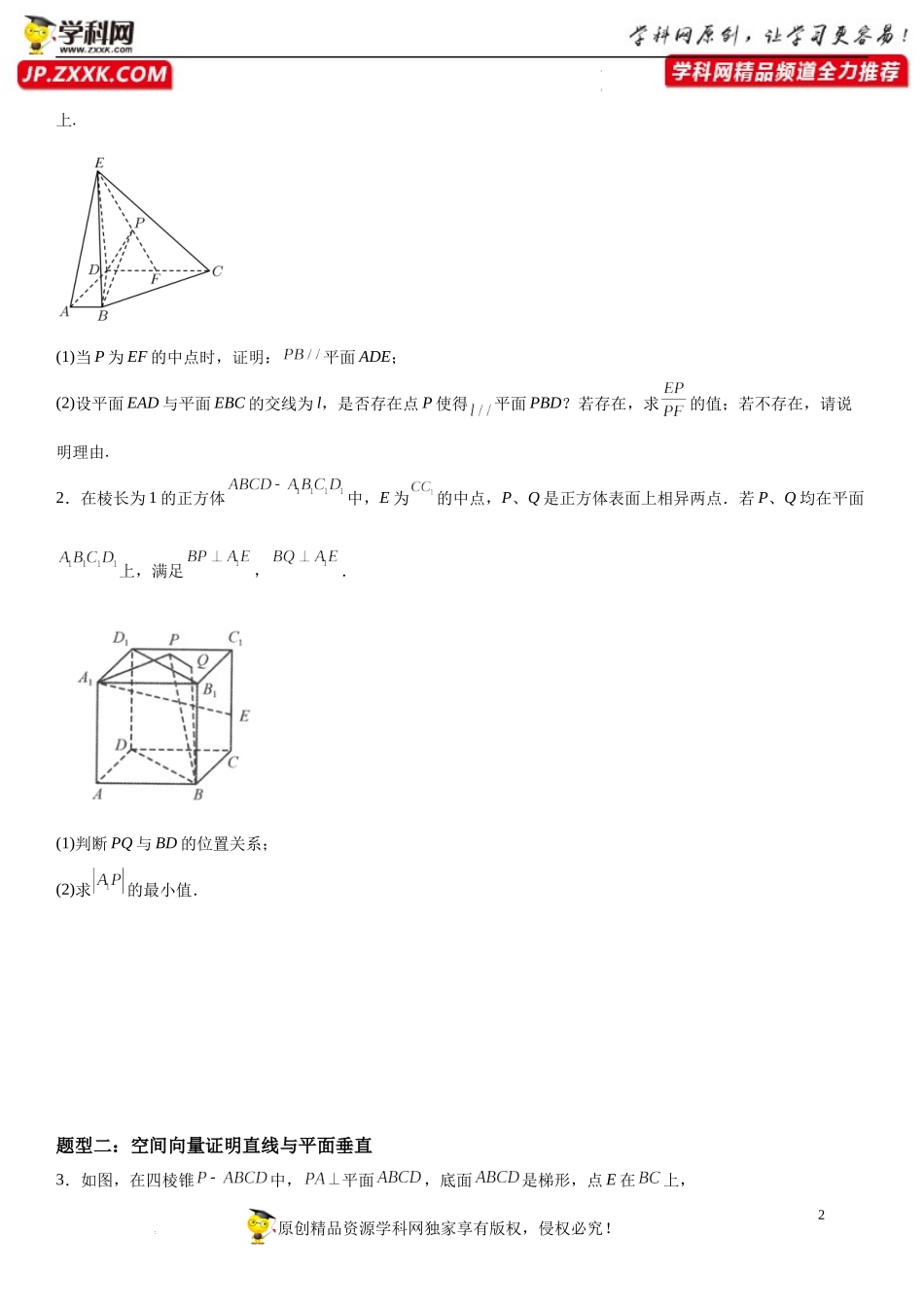
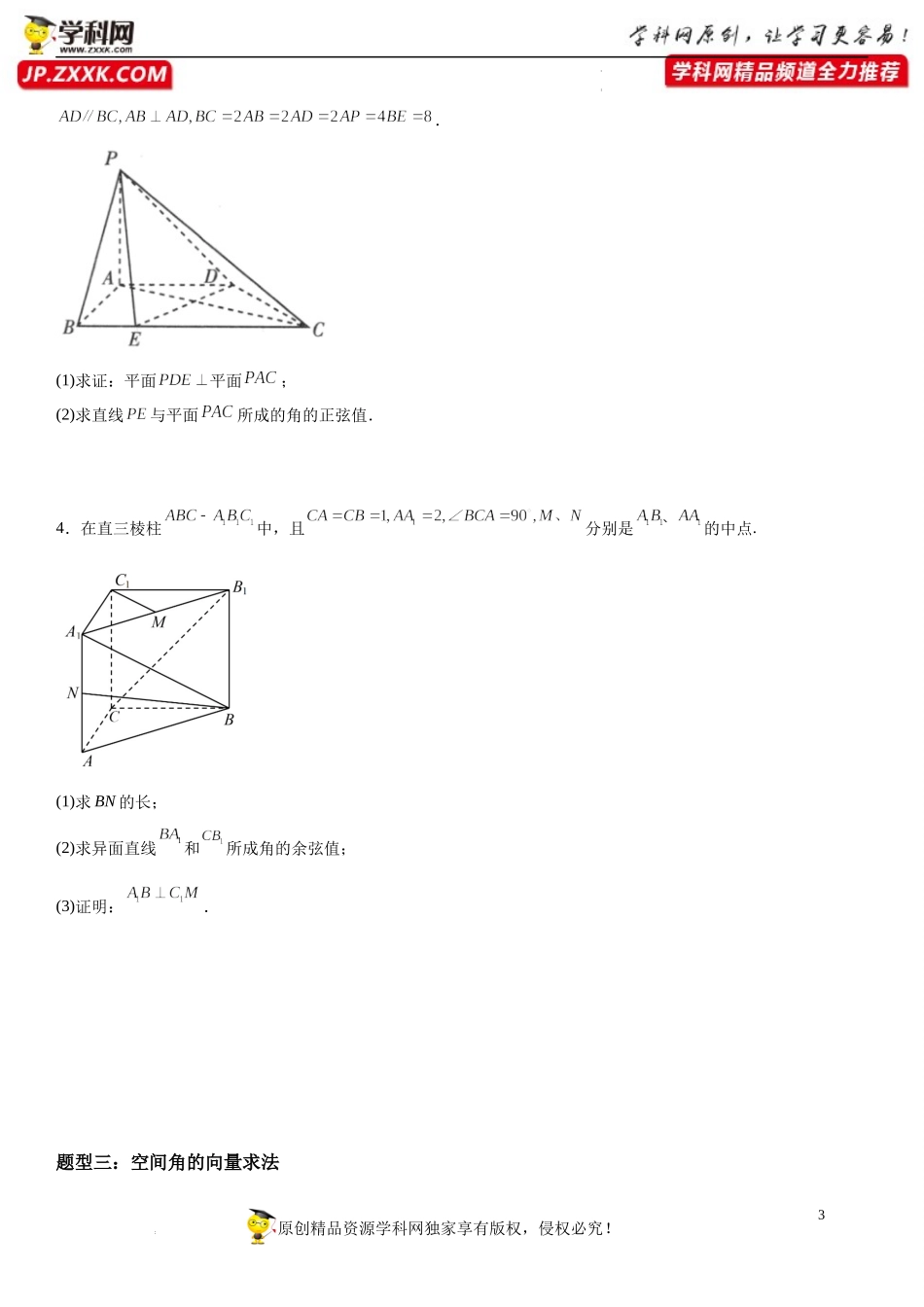
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司专题强化训练一:空间向量在直线、平面和角的应用【考点梳理】考点一:空间中直线、平面的平行1.线线平行的向量表示设u1,u2分别是直线l1,l2的方向向量,则l1∥l2⇔u1∥u2⇔∃λ∈R,使得u1=λu2.2.线面平行的向量表示设u是直线l的方向向量,n是平面α的法向量,l⊄α,则l∥α⇔u⊥n⇔u·n=0.面面平行的向量表示设n1,n2分别是平面α,β的法向量,则α∥β⇔n1∥n2⇔∃λ∈R,使得n1=λn2.考点二:空间中直线、平面的垂直1.线线垂直的向量表示设u1,u2分别是直线l1,l2的方向向量,则l1⊥l2⇔u1⊥u2⇔u1·u2=0.2.线面垂直的向量表示设u是直线l的方向向量,n是平面α的法向量,l⊄α,则l⊥α⇔u∥n⇔∃λ∈R,使得u=λn.知识点三面面垂直的向量表示设n1,n2分别是平面α,β的法向量,则α⊥β⇔n1⊥n2⇔n1·n2=0.考点三:角角的分类向量求法范围两条异面直线所成的角设两异面直线l1,l2所成的角为θ,其方向向量分别为u,v,则cosθ=|cos〈u,v〉|=直线与平面所成的角设直线AB与平面α所成的角为θ,直线AB的方向向量为u,平面α的法向量为n,则sinθ=|cos〈u,n〉|=两个平面的夹角设平面α与平面β的夹角为θ,平面α,β的法向量分别为n1,n2,则cosθ=|cos〈n1,n2〉|=【题型归纳】题型一:空间向量证明直线与平面平行1.如图,在四棱锥中,,,点F为棱CD的中点,与E,F相异的动点P在棱EF2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司上.(1)当P为EF的中点时,证明:平面ADE;(2)设平面EAD与平面EBC的交线为l,是否存在点P使得平面PBD?若存在,求的值;若不存在,请说明理由.2.在棱长为1的正方体中,E为的中点,P、Q是正方体表面上相异两点.若P、Q均在平面上,满足,.(1)判断PQ与BD的位置关系;(2)求的最小值.题型二:空间向量证明直线与平面垂直3.如图,在四棱锥中,平面,底面是梯形,点E在上,3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司.(1)求证:平面平面;(2)求直线与平面所成的角的正弦值.4.在直三棱柱中,且分别是的中点.(1)求BN的长;(2)求异面直线和所成角的余弦值;(3)证明:.题型三:空间角的向量求法4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)...