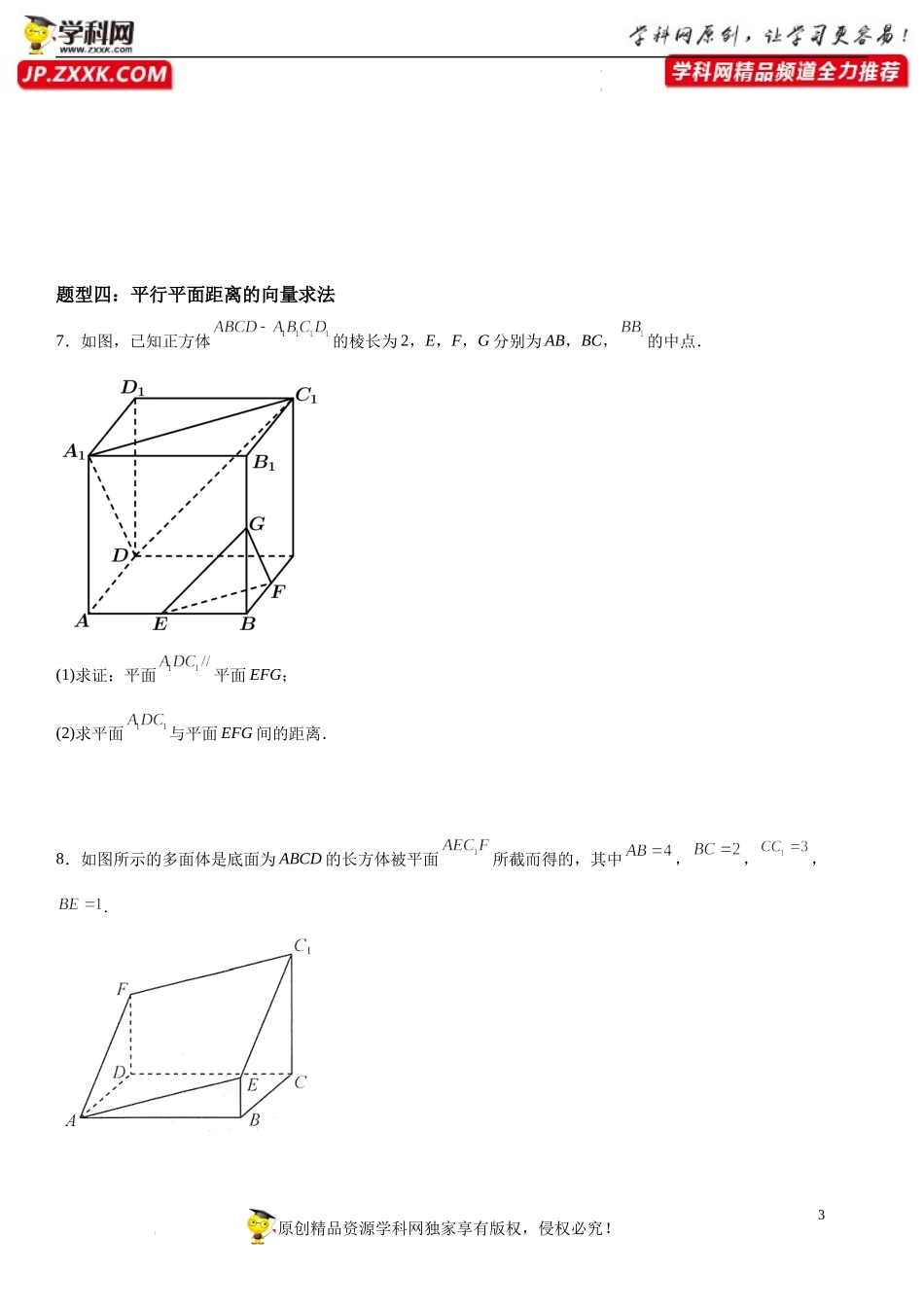
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司专题训练二:空间向量在点线面距离、存在性问题的应用【考点梳理】1.点P到直线l的距离已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点,设向量AP在直线l上的投影向量为AQ=a,则点P到直线l的距离为2.点P到平面α的距离设平面α的法向量为n,A是平面α内的定点,P是平面α外一点,则点P到平面α的距离为.【题型归纳】题型一:点到直线距离的向量求法1.在空间直角坐标系中,点关于轴的对称点为点,则点到直线的距离为()A.B.C.D.62.直线l的方向向量为,且l过点,则点到l的距离为()A.B.C.D.题型二:异面直线的向量求法3.在长方体中,,,,则异面直线与之间的距离是()A.B.C.D.4.定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司中,,,,则异面直线与之间的距离是()A.B.C.D.题型三:点到平面距离的向量求法5.如图,四棱锥中,侧面为等边三角形且垂直于底面,,,是的中点.(1)求到平面的距离;(2)点在棱上,且直线与底面所成角为,求二面角的正弦值.6.如图,在四面体中,平面,,,点在线段上.(1)当是线段中点时,求到平面的距离;(2)若二面角的余弦值为,求的值.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司题型四:平行平面距离的向量求法7.如图,已知正方体的棱长为2,E,F,G分别为AB,BC,的中点.(1)求证:平面平面EFG;(2)求平面与平面EFG间的距离.8.如图所示的多面体是底面为ABCD的长方体被平面所截而得的,其中,,,.4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司(1)求点C到平面的距离;(2)设过点平行于平面的平面为,求平面与平面之间的距离.题型五:空间向量的存在性问题9.如图,四边形是菱形,,平面平面,,,,.(1)证明:平面平面;(2)在棱上是否存在点使得平面与平面所成的锐二面角的余弦值为,若存在,求的值,若不存在,说明理由.10.如图1,在△MBC中,BM⊥BC,A,D分别为边MB,MC的中点,且BC=AM=2,将△MAD沿AD折起到△PAD的位置,使PA⊥AB,如图2,连结PB,PC.5原创精品资源学科网独家享有版权,侵权必究...