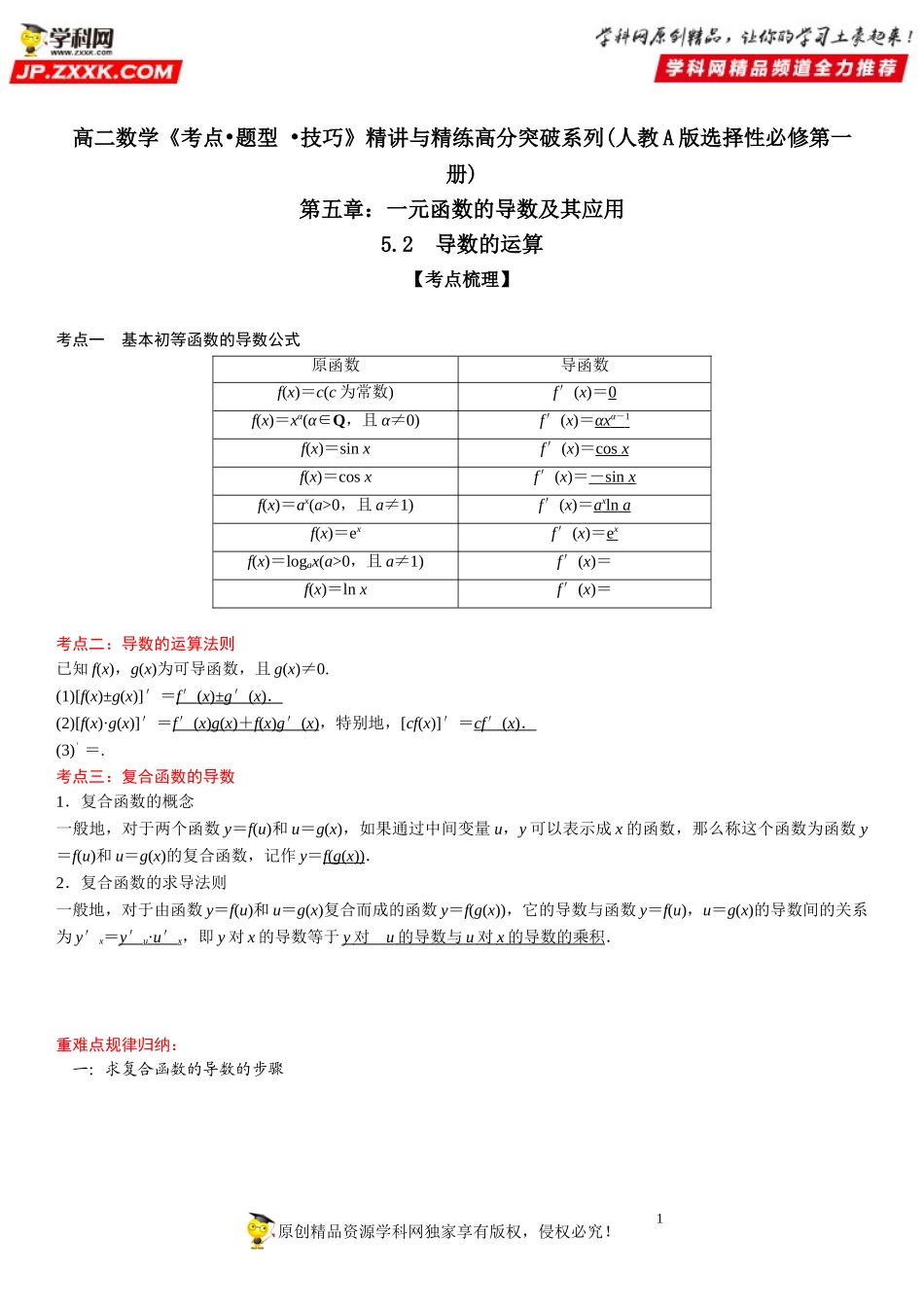
1高二数学《考点•题型•技巧》精讲与精练高分突破系列(人教A版选择性必修第一册)第五章:一元函数的导数及其应用5.2导数的运算【考点梳理】考点一基本初等函数的导数公式原函数导函数f(x)=c(c为常数)f′(x)=0f(x)=xα(α∈Q,且α≠0)f′(x)=αxα-1f(x)=sinxf′(x)=cosxf(x)=cosxf′(x)=-sinxf(x)=ax(a>0,且a≠1)f′(x)=axlnaf(x)=exf′(x)=exf(x)=logax(a>0,且a≠1)f′(x)=f(x)=lnxf′(x)=考点二:导数的运算法则已知f(x),g(x)为可导函数,且g(x)≠0.(1)[f(x)±g(x)]′=f′(x)±g′(x).(2)[f(x)·g(x)]′=f′(x)g(x)+f(x)g′(x),特别地,[cf(x)]′=cf′(x).(3)′=.考点三:复合函数的导数1.复合函数的概念一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).2.复合函数的求导法则一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为y′x=y′u·u′x,即y对x的导数等于y对u的导数与u对x的导数的乘积.重难点规律归纳:一:求复合函数的导数的步骤原创精品资源学科网独家享有版权,侵权必究!2二:利用导数的几何意义解决切线问题的两种情况①若已知点是切点,则在该点处的切线斜率就是该点处的导数;②若已知点不是切点,则应先设出切点,再借助两点连线的斜率公式进行求解.(2)求过点P与曲线相切的直线方程的三个步骤【题型归纳】题型一:利用导数公式求函数的导数1.(2021·全国·高二课时练习)求下列函数的导数:(1)(2)(3)(4)(5)(6)2.(2021·全国·高二课时练习)求下列函数的导数:(1)y=x-3;(2)y=3x;(3)y=log5x;(4);(5);(6)y=lnx;(7)y=ex.题型二:导数的运算法则原创精品资源学科网独家享有版权,侵权必究!33.(2021·江苏·高二专题练习)求下列函数的导数;(1)(2)(3)(4)(5)(6)4.(2021·全国·高二课时练习)求下列函数的导数:(1)y=x4-3x2-5x+6;(2)y=x·tanx;(3)y=(x+1)(x+2)(x+3);(4)y=.题型三:复合函数与导数的运算法则的综合应用5.(2021·全国·高二课时练习)求下列函数的导数:(1)(2)(3)(4)(5)(6)6.(2021·全国·高二课时练习)求下列函数的导数.(1)(2)(3);(4)(5)(6).原创精品资源学科网独家享有版权,侵权必究!4题型四:与切...