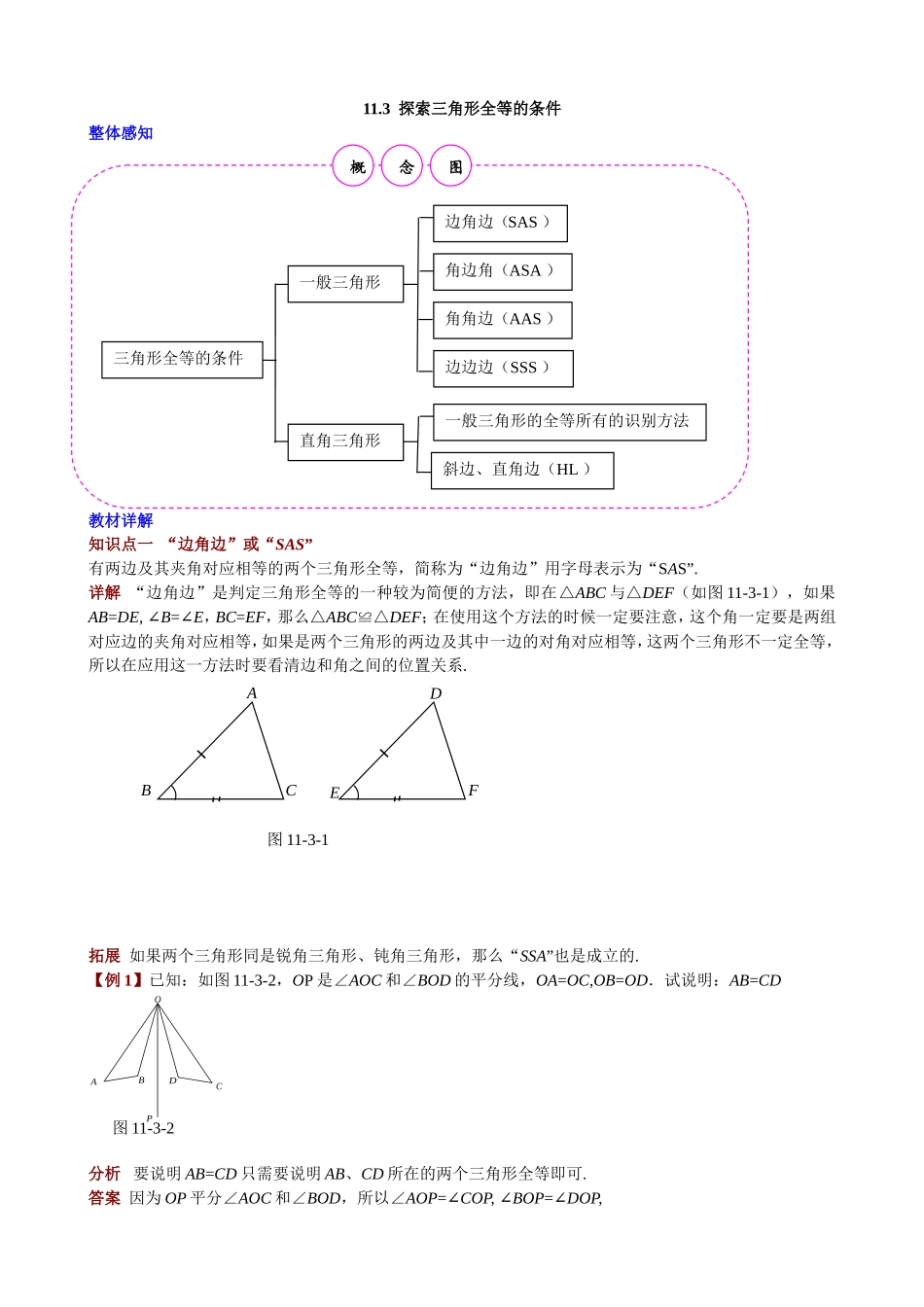
11.3探索三角形全等的条件整体感知教材详解知识点一“边角边”或“SAS”有两边及其夹角对应相等的两个三角形全等,简称为“边角边”用字母表示为“SAS”.详解“边角边”是判定三角形全等的一种较为简便的方法,即在△ABC与△DEF(如图11-3-1),如果AB=DE,∠B=∠E,BC=EF,那么△ABC≌△DEF;在使用这个方法的时候一定要注意,这个角一定要是两组对应边的夹角对应相等,如果是两个三角形的两边及其中一边的对角对应相等,这两个三角形不一定全等,所以在应用这一方法时要看清边和角之间的位置关系.拓展如果两个三角形同是锐角三角形、钝角三角形,那么“SSA”也是成立的.【例1】已知:如图11-3-2,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.试说明:AB=CD分析要说明AB=CD只需要说明AB、CD所在的两个三角形全等即可.答案因为OP平分∠AOC和∠BOD,所以∠AOP=∠COP,∠BOP=∠DOP,三角形全等的条件一般三角形直角三角形边角边(SAS)角边角(ASA)角角边(AAS)边边边(SSS)一般三角形的全等所有的识别方法斜边、直角边(HL)ABCDEF图11-3-1BACODP图11-3-2概念图所以∠AOB=∠COD在△AOB和△COD中,所以△AOB≌△COD,所以AB=CD.知识点二“角边角”或“ASA”有两角对应相等,且夹边相等的两个三角形全等.简称“角边角”公理,用字母表示为“ASA”.详解“角边角”是判定两个三角形全等另一种比较简便的方法,即在△ABC与△DEF(如图11-3-3)中,如果∠A=∠D,AB=DE,∠B=∠E,那么△ABC≌△DEF;(1)在使用这个方法的时候一定要注意,这条边应该是两个角的夹边对应相等,证明时要加强边角的对应关系.(2)在书写两个三角形全等时,一定要把夹边相等写在中间,以突出边角的位置感及对应关系.拓展当两个三角形中有两角相等,要说明这两三角形全等,只要说明这两角的夹边相等即可.【例2】如图11-3-4,D是AB上一点,DF交AC于点E,AE=EC,CF∥AB.试说明:AD=CF分析要说明AD=CF只需要说明AB、CD所在的两个三角形全等即可.解因为CF∥AB,所以∠A=∠ECF.在△AED和△CEF中,所以△AED≌△CEF,所以AD=CF.知识点三“角角边”AD图11-3-3BCEFABCDEF图11-3-4温馨提示:证明两两条线段相等,经常将它们放到两个三角形当中,然后根据条件证明对应边、对应角相等.温馨提示:本题关键是能通过CF∥AB得到∠A和∠ECF的相等,从而得到△ADE与△CFE的全等.有两角及其中一角的对边对应相等的两个三角形全等.简称“角角边”定理,用字母表示为“AAS”.详解“角角边”是判定两个三角形全...