1 空间直角坐标系.pptVIP免费

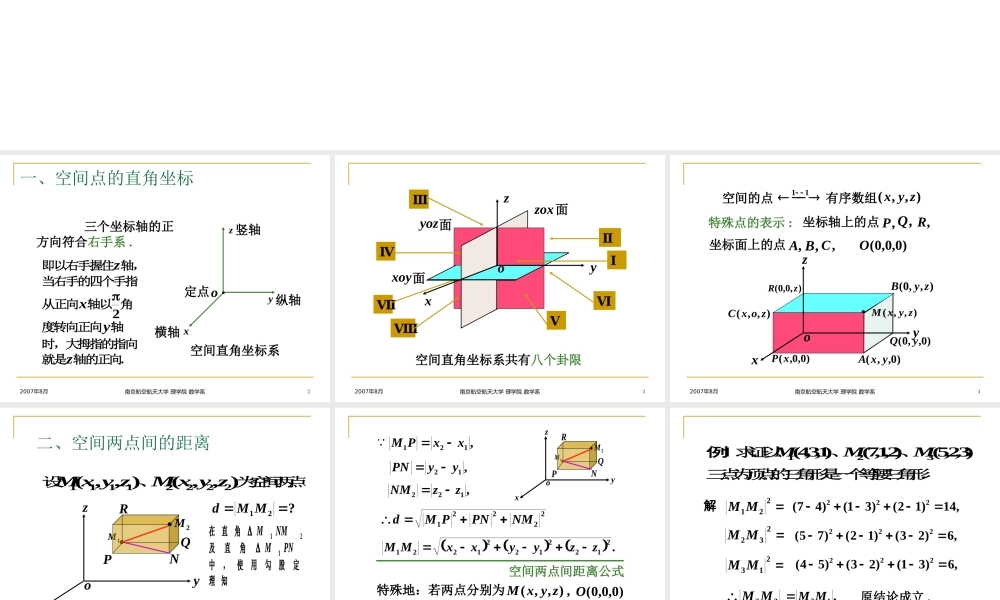
1空间直角坐标系空间点的直角坐标空间两点间的距离20078年月南京航空航天大学理学院数学系2x横轴y纵轴z竖轴定点o空间直角坐标系三个坐标轴的正方向符合右手系.即以右手握住z轴，当右手的四个手指从正向x轴以2角度转向正向y轴时，大拇指的指向就是z轴的正向.一、空间点的直角坐标20078年月南京航空航天大学理学院数学系3Ⅶxyozxoy面yoz面zox面空间直角坐标系共有八个卦限ⅠⅡⅢⅣⅤⅥⅧ20078年月南京航空航天大学理学院数学系4空间的点有序数组),,(zyx11特殊点的表示:)0,0,0(O),,(zyxMxyzo)0,0,(xP)0,,0(yQ),0,0(zR)0,,(yxA),,0(zyB),,(zoxC坐标轴上的点,P,Q,R坐标面上的点,A,B,C20078年月南京航空航天大学理学院数学系5设),,(1111zyxM、),,(2222zyxM为空间两点xyzo1MPNQR2M?21MMd在直角21NMM及直角PNM1中，使用勾股定理知,222212NMPNPMd二、空间两点间的距离20078年月南京航空航天大学理学院数学系6,121xxPM,12yyPN,122zzNM22221NMPNPMd.21221221221zzyyxxMM空间两点间距离公式特殊地：若两点分别为,),,(zyxM)0,0,0(OOMd.222zyxxyzo1MPNQR2M20078年月南京航空航天大学理学院数学系7例1求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M三点为顶点的三角形是一个等腰三角形.解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立.20078年月南京航空航天大学理学院数学系8例2设P在x轴上，它到)3,2,0(1P的距离为到点)1,1,0(2P的距离的两倍，求点P的坐标.解设P点坐标为),0,0,(x因为P在x轴上，1PP22232x,112x2PP22211x,22x1PP,22PP112x222x,1x所求点为).0,0,1(),0,0,1(20078年月南京航空航天大学理学院数学系9空间直角坐标系空间两点间距离公式（注意它与平面直角坐标系的区别）（轴、面、卦限）三、小结21221221221zzyyxxMM20078年月南京航空航天大学理学院数学系10思考题在空间直角坐标系中，指出下列各点在哪个卦限？,)3,2,1(A,)4,3,2(B,)4,3,2(C.)1,3,2(D20078年月南京航空航天大学理学院数学系11思考题解答A:;B:;C:;D:;ⅣⅤⅧⅢ20078年月南京航空航天大学理学院数学系121、下列各点所在象限分别是：_______;1,3,2d________4,3,2c________4,3,2b_________3,2...