第6课时 相似三角形的性质.pptVIP免费

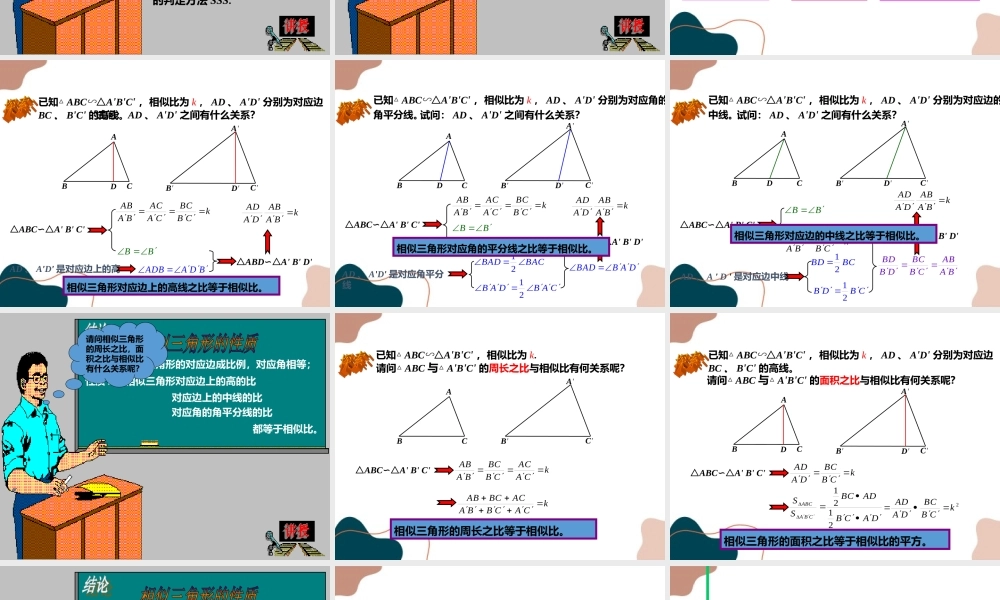
第23章图形的相似23.3相似三角形第6课时相似三角形的性质平行于三角形一边的直线，和其他两边（或两边的延长线）相交所构成的三角形和原三角形相似。 DE//BCBCADEABCDE∴△ADE∽△ABC“A”型“X”型这是我们以后经常研究的两种基本图形。两角分别相等的两个三角形相似。ABCFDE ∠A=∠D，∠B=∠E∴△ABC∽△DEFDADFACDEAB，两边成比例且夹角相等的两个三角形相似。ABCFDE ∴△ABC∽△DEF角一定是两边的夹角哟！EFBCDFACDEAB三边成比例的两个三角形相似。ABCFDE ∴△ABC∽△DEF当相似比为1时，即是全等三角形的判定方法SSS.长长中中短短相似三角形的对应边成比例，对应角相等。ABCFDE △ABC∽△DEF∴∠A=∠D∠B=∠E∠C=∠FDFACEFBCDEAB回顾：三角形的三条重要线段是什么？CBADEFCBA●CBA请你阐述这三条线段各自所具有的性质？BCCEBE21BACCAFBAF2190ADCADB已知△ABC∽△A'B'C'，相似比为k，AD、A'D'分别为对应边BC、B'C'的高线。kCBBCCAACBAAB试问：AD、A'D'之间有什么关系？A'B'C'D'ABCDBBAD、A'D'是对应边上的高△ABC∽△A'B'C'BDAADB△ABD∽△A'B'D'kBAABDAAD相似三角形对应边上的高线之比等于相似比。已知△ABC∽△A'B'C'，相似比为k，AD、A'D'分别为对应角的角平分线。kCBBCCAACBAAB试问：AD、A'D'之间有什么关系？BBAD、A'D'是对应角平分线△ABC∽△A'B'C'BACBAD21△ABD∽△A'B'D'kBAABDAADA'B'C'D'ABCDCABBACCABDAB21DABBAD相似三角形对应角的平分线之比等于相似比。已知△ABC∽△A'B'C'，相似比为k，AD、A'D'分别为对应边的中线。kCBBCBAAB试问：AD、A'D'之间有什么关系？BBAD、A'D'是对应边中线△ABC∽△A'B'C'BCBD21△ABD∽△A'B'D'kBAABDAADCBDB21BAABCBBCDBBDA'B'C'D'ABCD相似三角形对应边的中线之比等于相似比。性质1：相似三角形的对应边成比例，对应角相等；性质2：相似三角形对应边上的高的比对应边上的中线的比对应角的角平分线的比都等于相似比。请问相似三角形的周长之比，面积之比与相似比有什么关系呢？已知△ABC∽△A'B'C'，相似比为k.A'B'C'ABC请问△ABC与△A'B'C'的周长之比与相似比有何关系呢？△ABC∽△A'B'C'kCAACCBBCBAABkCACBBAACBCAB...