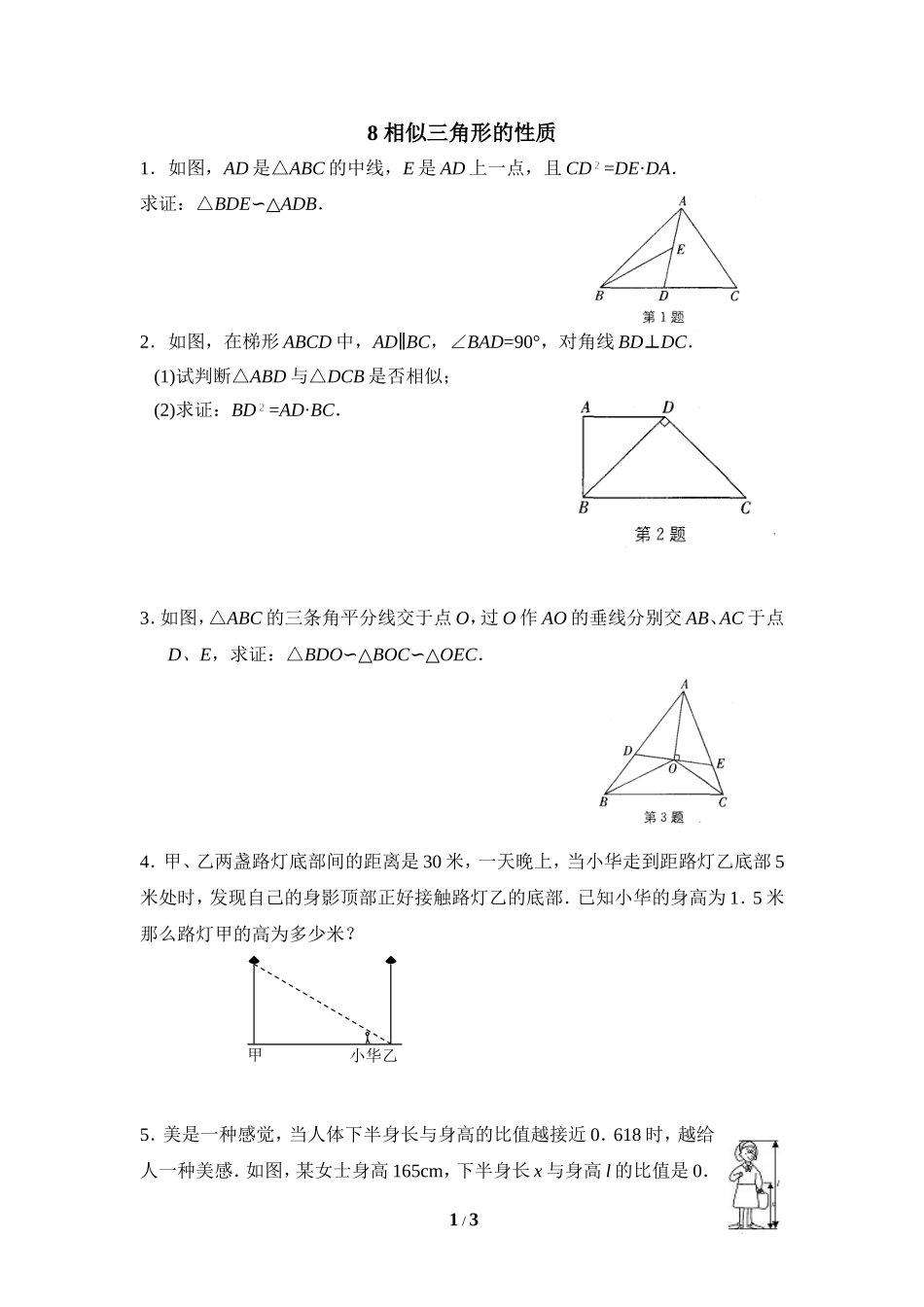
8相似三角形的性质1.如图,AD是△ABC的中线,E是AD上一点,且CD=DE·DA.求证:△BDE∽△ADB.2.如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.(1)试判断△ABD与△DCB是否相似;(2)求证:BD=AD·BC.3.如图,△ABC的三条角平分线交于点O,过O作AO的垂线分别交AB、AC于点D、E,求证:△BDO∽△BOC∽△OEC.4.甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米那么路灯甲的高为多少米?5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.1/3甲小华乙60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为()A.4cmB.6cmC.8cmD.10cm6.如图,梯形ABCD中,ABCD∥,点F在BC上,连DF与AB的延长线交于点G.(1)求证:CDFBGF△∽△;(2)当点F是BC的中点时,过F作EFCD∥交AD于点E,6cm4cmABEF,求CD的长.2/3DCFEABG参考答案1.点拨:由BD=CD,CD=DE·DA,可得BD=DE·DA,即证.2.(1)△ABD与△DCB相似(2)略3.点拨:OB平分∠ABC,OC平分∠ACB,∠BOC=90°+∠BAC.又AO⊥DE,且∠DAO=∠EAO,∠BDO=90°+∠BAC.∠BDO=∠BOC,△BDO∽△BOC.同理可证△BOC∽△OEC.4.解析:本题考查相似的有关知识,设路灯高为米,由相似得,解得,所以路灯甲的高为9米.5.C6.解析:由平行条件很容易就能得到相似,第一问很好解决;第二问要充分利用中点找到全等三角形,把CD转化为BG来解决问题.证明:(1)∵梯形ABCD,ABCD∥,∴CDFFGBDCFGBF,,∴CDFBGF△∽△.(2)由(1)CDFBGF△∽△,又F是BC的中点,BFFC∴CDFBGF△≌△,∴DFFGCDBG,又∵EFCD∥,ABCD∥,∴EFAG∥,得2EFBGABBG.∴22462BGEFAB,∴2cmCDBG.3/3