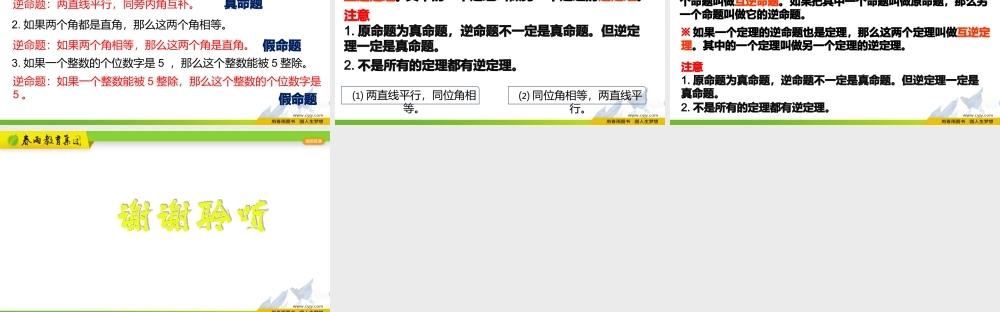
学习任务理解互逆命题和互逆定理的概念?会写出一个命题的逆命题?命题有真有假。正确的命题是真命题,错误的命题是假命题。什么是命题?表示判断一件事情的语句,叫做命题。命题可看做由题设(或条件)和结论两部分组成。命题由哪两部分组成?定理:定理是命题,而且是真命题。复习回顾假a=ba2=b2⑷如果a2=b2,那么a=b。真a2=b2a=b⑶如果a=b,那么a2=b2。真两直线平行同位角相等⑵同位角相等,两直线平行。真同位角相等两直线平行⑴两直线平行,同位角相等。真假结论条件命题观察表中的命题,命题⑴与命题⑵有什么关系?命题⑶与命题⑷呢?知识精讲一般来说,在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。知识精讲⑵同位角相等,两直线平行。⑴两直线平行,同位角相等。原命题逆命题互为逆命题指出下列命题的题设和结论,并说出它们的逆命题。1.如果一个三角形是直角三角形,那么它的两个锐角互余。题设:一个三角形是直角三角形。结论:它的两个锐角互余。逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形。典例解析结论:它的每个角都等于60°。题设:一个三角形是等边三角形。指出下列命题的题设和结论,并说出它们的逆命题。2.等边三角形的每个角都等于60°。典例解析逆命题:如果一个三角形的每个角都等于60°,那么这个三角形是等边三角形。指出下列命题的题设和结论,并说出它们的逆命题。3.全等三角形的对应角相等。题设:两个三角形是全等三角形。结论:它们的对应角相等。逆命题:如果两个三角形的对应角相等,那么这两个三角形全等。典例解析指出下列命题的题设和结论,并说出它们的逆命题。4.到一个角的两边距离相等的点,在这个角的平分线上。题设:一个点到一个角的两边距离相等。结论:它在这个角的平分线上。逆命题:角平分线上一点到角两边的距离相等。典例解析指出下列命题的题设和结论,并说出它们的逆命题。5.线段的垂直平分线上的点到这条线段的两个端点的距离相等。题设:一个点在一条线段的垂直平分线上。结论:它到这条线段的两个端点的距离相等。逆命题:到一条线段的两个端点的距离相等的点在这条线段的垂直平分线上。典例解析写出下列命题的逆命题,并判断是真命题还是假命题。1.同旁内角互补,两直线平行。2.如果两个角都是直角,那么这...