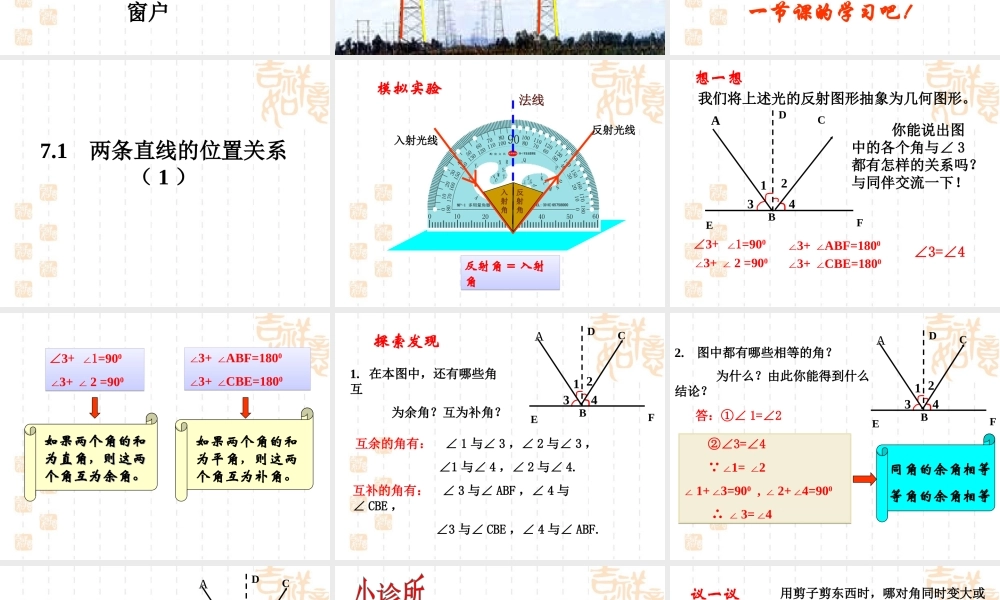
第七章相交线与平行线窗户生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。在这一章里,我们将发现相交线和平行线的一些特征,并探索两条直线平行的条件。我们还将利用圆规和没有刻度的直尺,尝试着作一些美丽的图案!让我们一起进入第一节课的学习吧!7.1两条直线的位置关系(1)反射角=入射角反射角=入射角入射角反射角入射光线反射光线法线模拟实验我们将上述光的反射图形抽象为几何图形。你能说出图中的各个角与∠3都有怎样的关系吗?与同伴交流一下!142C3ADBEF∠3=∠4想一想∠3+2=90∠0∠3+∠1=900∠3+CBE=180∠0∠3+ABF=180∠0如果两个角的和如果两个角的和为直角,则这两为直角,则这两个角互为余角。个角互为余角。如果两个角的和为平角,则这两个角互为补角。∠3+∠1=900∠3+2=90∠0∠3+∠1=900∠3+2=90∠0∠3+ABF=180∠0∠3+CBE=180∠0∠3+ABF=180∠0∠3+CBE=180∠03412CABDEF1.在本图中,还有哪些角互为余角?互为补角?互余的角有:∠1与∠3,∠2与∠3,∠1与∠4,∠2与∠4.互补的角有:∠3与∠ABF,∠4与∠CBE,∠3与∠CBE,∠4与∠ABF.探索发现2.图中都有哪些相等的角?为什么?由此你能得到什么结论?答:①∠1=∠2同角的余角相等等角的余角相等3412CABDEF②∠3=∠4 ∠1=2∠∠1+3=90∠0,2+4=90∠∠0∴∠3=4∠②∠3=∠4 ∠1=2∠∠1+3=90∠0,2+4=90∠∠0∴∠3=4∠③∠ABF=∠CBE ∠3=4∠∠ABF+3=180∠0,CBE+4=180∠∠0∴∠ABF=CBE∠③∠ABF=∠CBE ∠3=4∠∠ABF+3=180∠0,CBE+4=180∠∠0∴∠ABF=CBE∠3412CABDEF同角的补角相等等角的补角相等同角的补角相等等角的补角相等(1)300,700与800的和为平角,所以这三个角互余()(2)一个角的余角必为锐角。()(3)一个角的补角必为钝角。()(4)90的角为余角。()(5)两角是否互补既与其大小有关又与其位置有关()×√×××判断下列说法是否正确00互余与互补是指两个角之间的数量关系,与它们的位置关系无关。注意:用剪子剪东西时,哪对角同时变大或变小?你能说明理由吗?12ADCBO在图2中,还有相等的角吗?这几组相等的角在位置上有什么样的关系,你能试着描述一下吗?像∠1与∠2,∠AOC与∠BOD一样,两个角有公共的顶点,且一个角的两边是另一角两边的延长线,这两个角互为对顶角。性质:对顶角相等 ∠1+AOC=180∠0∠2+∠AOC=1800∴1=2(∠∠同角的补角相等)议一议1.你能举出生活中包含对顶角的例子吗?BOAOC12C’...