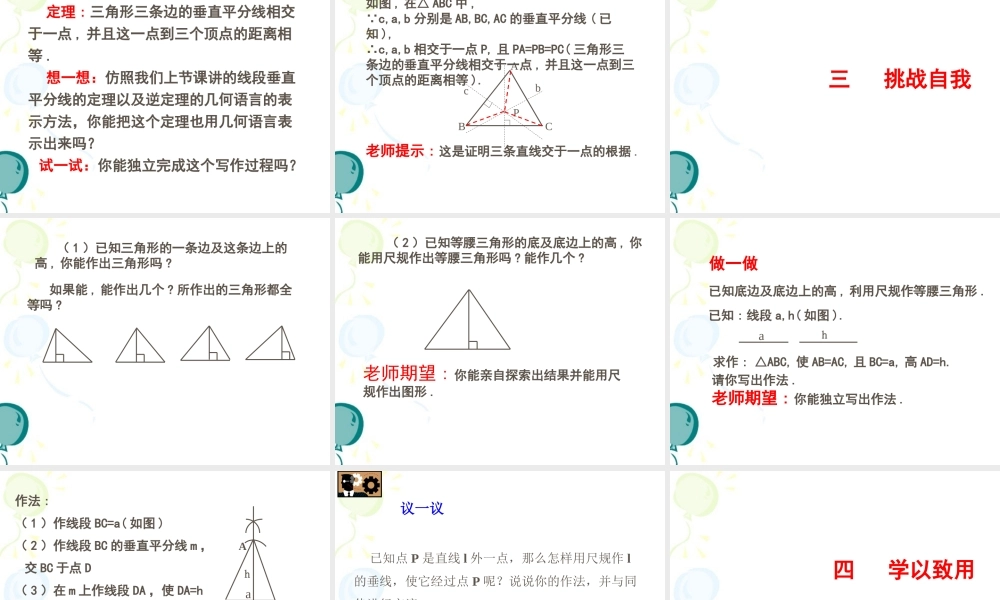
线段的垂直平分线(2)一回顾与思考定理:线段垂直平分线上的点到这条线段两个端点的距离相等老师提示:这个结论是经常用来证明两条线段相等的根据之一.NACBPM如图, AC=BC,MN⊥AB,P是MN上任意一点(已知),∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).逆定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.几何语言描述:如图, PA=PB(已知),∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.ABP已知:线段AB,(如图).求作:线段AB的垂直平分线.作法:回顾思考:用尺规作线段的垂直平分线.1.分别以点A和B为圆心,以大AB/2长为半径作弧,两弧交于点C和D.ABCD2.作直线CD.则直线CD就是线段AB的垂直平分线.想一想:请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.特别提示:因为直线CD与线段AB的交点就是AB的中点,所以以后我们经常也会用这种方法作线段的中点.二学习新知剪一个三角形纸片通过折叠找出每条边的垂直平分线.观察这三条垂直平分线,你发现了什么?结论:三角形三条边的垂直平分线相交于一点.你想证明这个命题吗?你能证明这个命题吗?老师期望:你能写出规范的证明过程.利用尺规作出三角形三条边的垂直平分线.再观察这三条垂直平分线,你又发现了什么?与同伴交流.结论:三角形三条边的垂直平分线相交于一点.你想证明这个命题吗?你能证明这个命题吗?老师期望:你能写出规范的证明过程.如何证三条直线交于一点?命题:三角形三条边的垂直平分线相交于一点.基本想法是这样的:我们知道,两条直线相交只有一个交点。要想证明三条直线相交于一点只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学到的逆定理.如图,在△ABC中,设AB,BC的垂直平分线相交于点P,连接AP,BP,CP. 点P在线段AB的垂直平分线上,∴PA=PB.同理,PB=PC.∴PA=PC.∴点P在线段AC的垂直平分线上,∴AB,BC,AC的垂直平分线相交于一点.ABCP定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.想一想:仿照我们上节课讲的线段垂直平分线的定理以及逆定理的几何语言的表示方法,你能把这个定理也用几何语言表示出来吗?试一试:你能独立完成这个写作过程吗?老师提示:这是证明三条直线交于一点的根据.如图,在△ABC中, c,a,b分别是AB,BC,AC的垂直平分线(已知),∴c,a,b相交于一点P,且PA=PB=PC(三角形三条边的垂直平分线相交于...