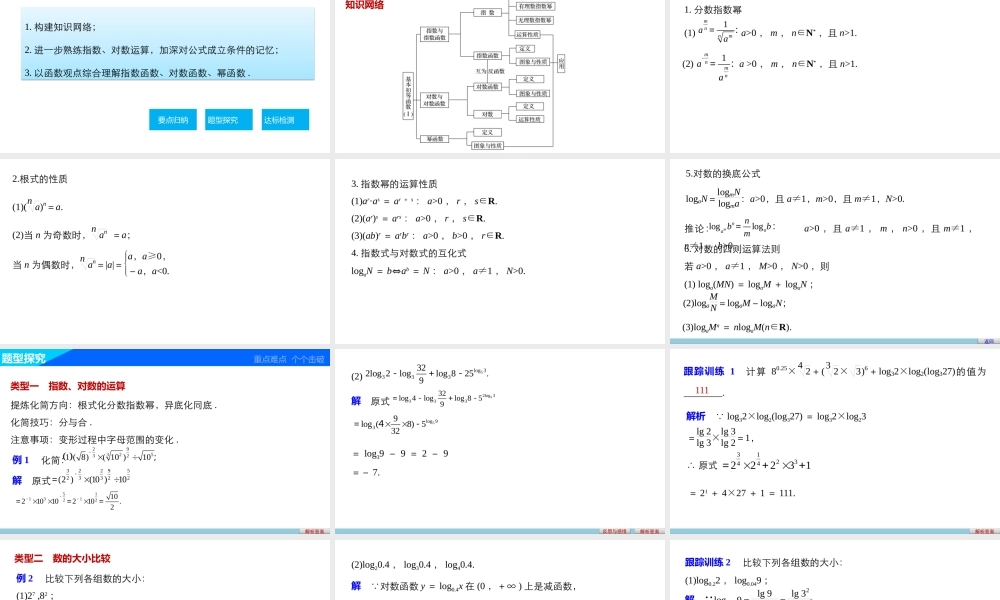
章末复习课第二章基本初等函数(Ⅰ)1.构建知识网络;2.进一步熟练指数、对数运算,加深对公式成立条件的记忆;3.以函数观点综合理解指数函数、对数函数、幂函数.要点归纳题型探究达标检测学习目标知识网络要点归纳主干梳理点点落实1.分数指数幂知识梳理(1)a>0,m,n∈N*,且n>1.1mnnmaa=:(2)a>0,m,n∈N*,且n>1.-1mnmnaa=:2.根式的性质(1)(na)n=a.(2)当n为奇数时,nan=a;当n为偶数时,nan=|a|=a,a≥0,-a,a<0.3.指数幂的运算性质(1)ar·as=ar+s:a>0,r,s∈R.(2)(ar)s=ars:a>0,r,s∈R.(3)(ab)r=arbr:a>0,b>0,r∈R.4.指数式与对数式的互化式logaN=b⇔ab=N:a>0,a≠1,N>0.返回推论:a>0,且a≠1,m,n>0,且m≠1,n≠1,b>0.5.对数的换底公式logaN=logmNlogma:a>0,且a≠1,m>0,且m≠1,N>0.loglogmnaanbbm=:6.对数的四则运算法则若a>0,a≠1,M>0,N>0,则(1)loga(MN)=logaM+logaN;(2)logaMN=logaM-logaN;(3)logaMn=nlogaM(n∈R).类型一指数、对数的运算题型探究重点难点个个击破提炼化简方向:根式化分数指数幂,异底化同底.化简技巧:分与合.注意事项:变形过程中字母范围的变化.解析答案例1化简:29325321(8)(10)10;解原式2239533222(2)(10)10-=51131221021010210.2---===解原式解析答案5log3333322log2loglog825.9-+-52log333332log4loglog859=-+-5log939log(8)532=4-=log39-9=2-9=-7.反思与感悟(2)解析 log32×log2(log327)=log32×log23跟踪训练1计算80.25×42+(32×3)6+log32×log2(log327)的值为________.解析答案=lg2lg3×lg3lg2=1,∴原式31234422231=++=21+4×27+1=111.111类型二数的大小比较例2比较下列各组数的大小:(1)27,82;解析答案解 82=(23)2=26,由指数函数y=2x在R上单调递增知26<27即82<27.(2)log20.4,log30.4,log40.4.∴1log0.42<1log0.43<1log0.44,解析答案解 对数函数y=log0.4x在(0,+∞)上是减函数,∴log0.44log0.23,即log0.22>log0.049.(2)a1.2,a1.3;解析答案解 函数y=ax(a>0且a≠1...