27.2.2 相似三角形的性质.pptVIP免费

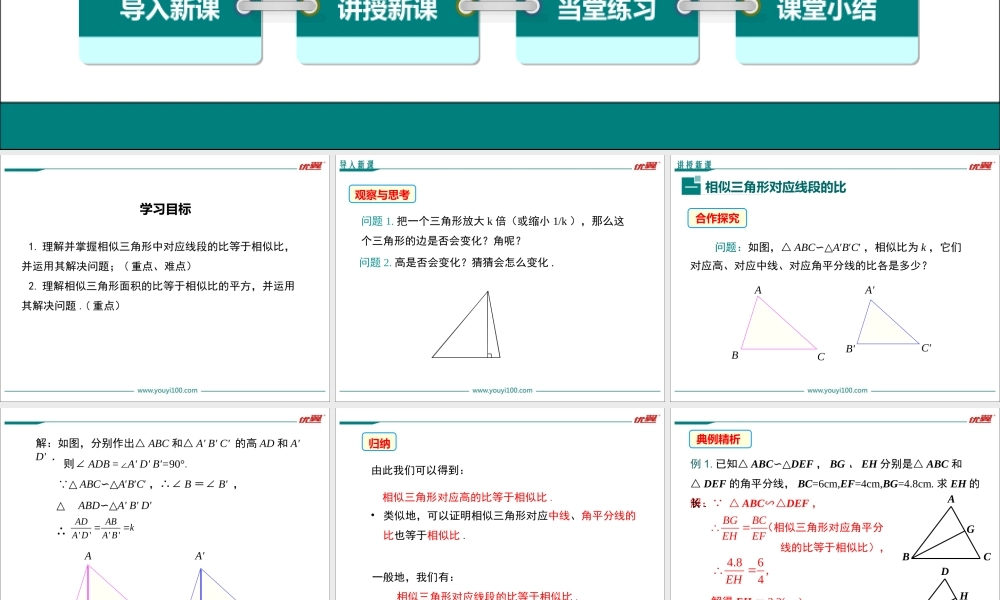
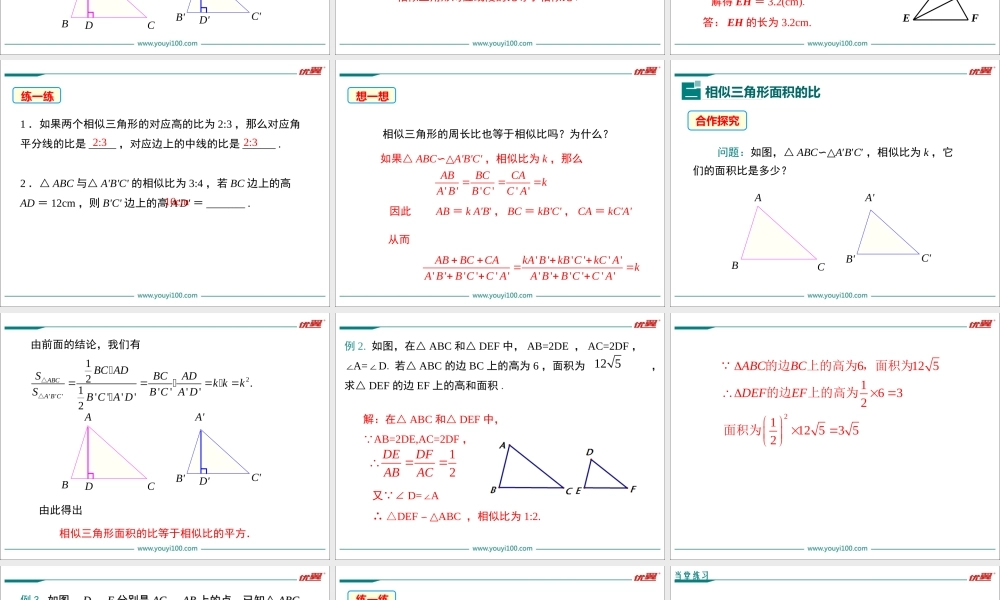
27.2相似三角形第二十七章相似优翼课件导入新课讲授新课当堂练习课堂小结学练优九年级数学下（RJ）教学课件27.2.2相似三角形的性质1.理解并掌握相似三角形中对应线段的比等于相似比，并运用其解决问题；(重点、难点）2.理解相似三角形面积的比等于相似比的平方，并运用其解决问题.(重点）学习目标导入新课观察与思考问题1.把一个三角形放大k倍（或缩小1/k），那么这个三角形的边是否会变化？角呢？问题2.高是否会变化？猜猜会怎么变化.问题：如图，△ABC∽△A′B′C′，相似比为k，它们对应高、对应中线、对应角平分线的比各是多少？讲授新课相似三角形对应线段的比一合作探究ABCA'B'C'解：如图，分别作出△ABC和△A'B'C'的高AD和A'D'．则∠ADB=∠A'D'B'=90°.△ABD∽△A'B'D'ABCA'B'C'D'D △ABC∽△A′B′C′，∴∠B＝∠B'，''''ADABkADAB∴•类似地，可以证明相似三角形对应中线、角平分线的比也等于相似比.由此我们可以得到：归纳相似三角形对应高的比等于相似比.一般地，我们有：相似三角形对应线段的比等于相似比.解： △ABC∽△DEF，解得EH＝3.2(cm).答：EH的长为3.2cm.DEFH（相似三角形对应角平分线的比等于相似比），例1.已知△ABC∽△DEF，BG、EH分别是△ABC和△DEF的角平分线，BC=6cm,EF=4cm,BG=4.8cm.求EH的长.BGBCEHEF4.86,4EH典例精析AGBC1．如果两个相似三角形的对应高的比为2:3，那么对应角平分线的比是_____，对应边上的中线的比是______.2．△ABC与△A'B'C'的相似比为3:4，若BC边上的高AD＝12cm，则B'C'边上的高A'D'＝_______.2:32:316cm练一练想一想相似三角形的周长比也等于相似比吗？为什么？如果△ABC∽△A'B'C'，相似比为k，那么''''''ABBCCAkABBCCA因此AB＝kA'B'，BC＝kB'C'，CA＝kC'A'从而''''''''''''''''''ABBCCAkABkBCkCAkABBCCAABBCCA相似三角形面积的比二合作探究问题：如图，△ABC∽△A′B′C′，相似比为k，它们的面积比是多少？ABCA'B'C'ABCA'B'C'D'D由前面的结论，我们有2'''12.1''''''''2ABCABCBCADSBCADkkkSBCADBCAD△△相似三角形面积的比等于相似比的平方．由此得出例2.如图，在△ABC和△DEF中，AB=2DE，AC=2DF，∠A=∠D.若△ABC的边BC上的高为6，面积为，求△DEF的边EF上的高和面积.125解：在△ABC和△DEF中， AB=2DE,AC=2DF，12DEDFABAC又 ∠D=A∠∴△DEF∽ABC△，相似比为1:2.2612516321125352ABCBCDEFEF的...