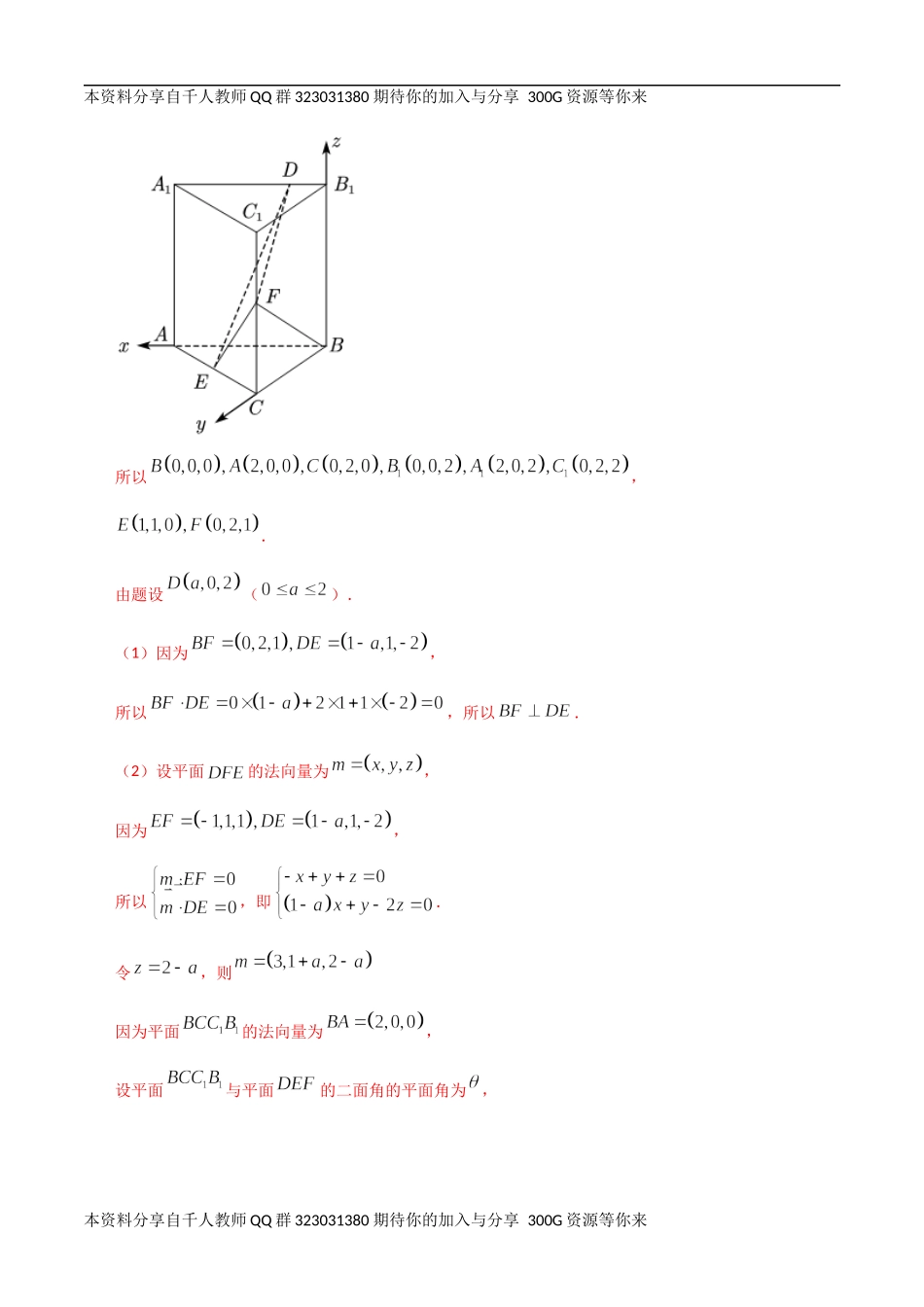
本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来2012-2021十年全国高考数学真题分类汇编立体几何大题(精解精析)一、解答题1.(2021年高考全国甲卷理科)已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.(1)证明:;(2)当为何值时,面与面所成的二面角的正弦值最小?【答案】(1)见解析;(2)解析:因为三棱柱是直三棱柱,所以底面,所以因为,,所以,又,所以平面.所以两两垂直.以为坐标原点,分别以所在直线为轴建立空间直角坐标系,如图.本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来所以,.由题设().(1)因为,所以,所以.(2)设平面的法向量为,因为,所以,即.令,则因为平面的法向量为,设平面与平面的二面角的平面角为,本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来则.当时,取最小值为,此时取最大值为.所以,此时.【点睛】本题考查空间向量的相关计算,能够根据题意设出(),在第二问中通过余弦值最大,找到正弦值最小是关键一步.2.(2021年高考全国乙卷理科)如图,四棱锥的底面是矩形,底面,,为的中点,且.(1)求;(2)求二面角的正弦值.本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来【答案】(1);(2)解析:(1)平面,四边形为矩形,不妨以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,设,则、、、、,则,,,则,解得,故;(2)设平面的法向量为,则,,由,取,可得,本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来本资料分享自千人教师QQ群323031380期待你的加入与分享300G资源等你来设平面的法向量为,,,由,取,可得,,所以,,因此,二面角的正弦值为.【点睛】思路点睛:利用空间向量法求解二面角的步骤如下:(1)建立合适的空间直角坐标系,写出二面角对应的两个半平面中对应的点的坐标;(2)设出法向量,根据法向量垂直于平面内两条直线的方向向量,求解出平面的法向量(注:若半平面为坐标平面,直接取法向量即可);(3)计算(2)中两个法向量...