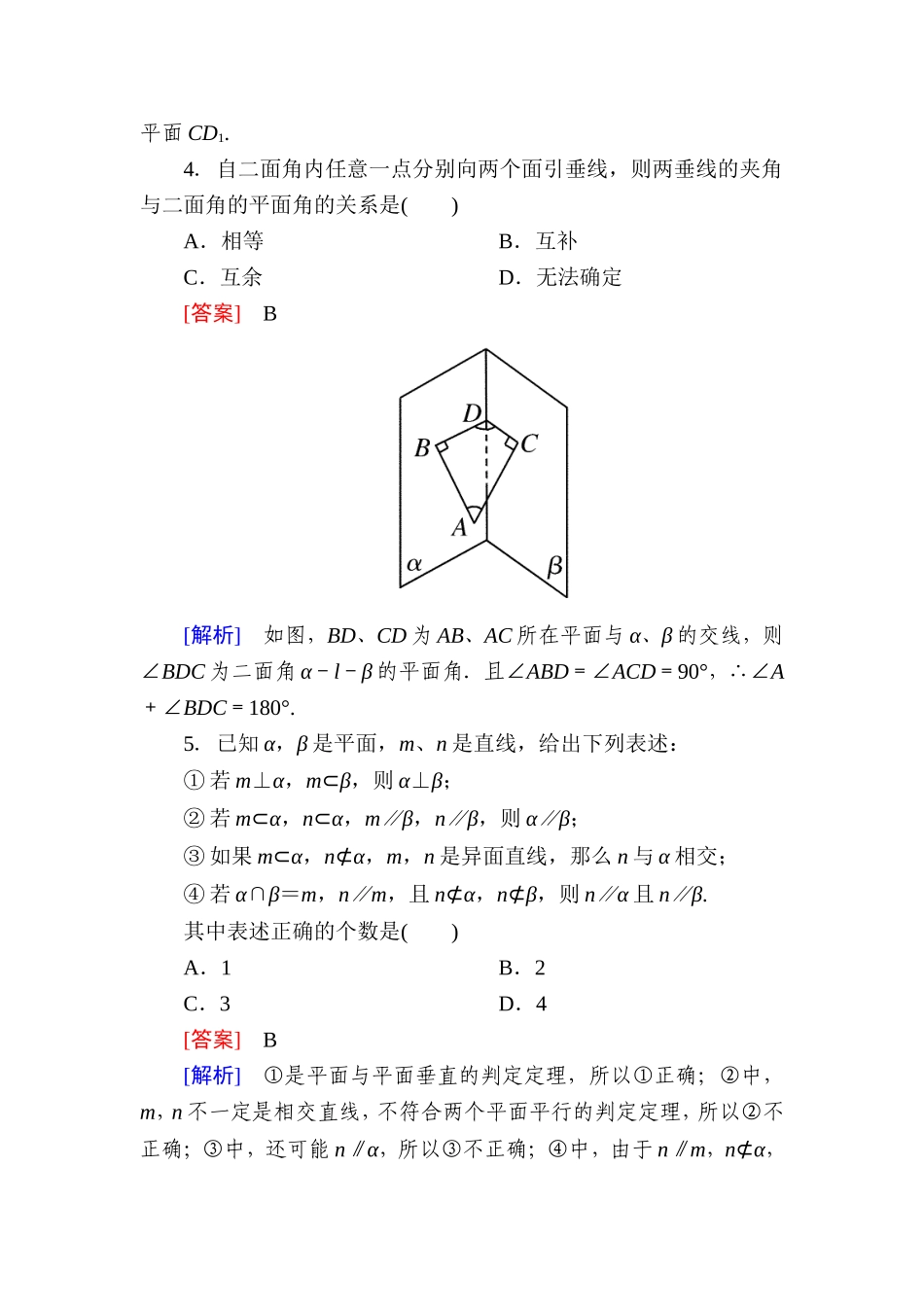
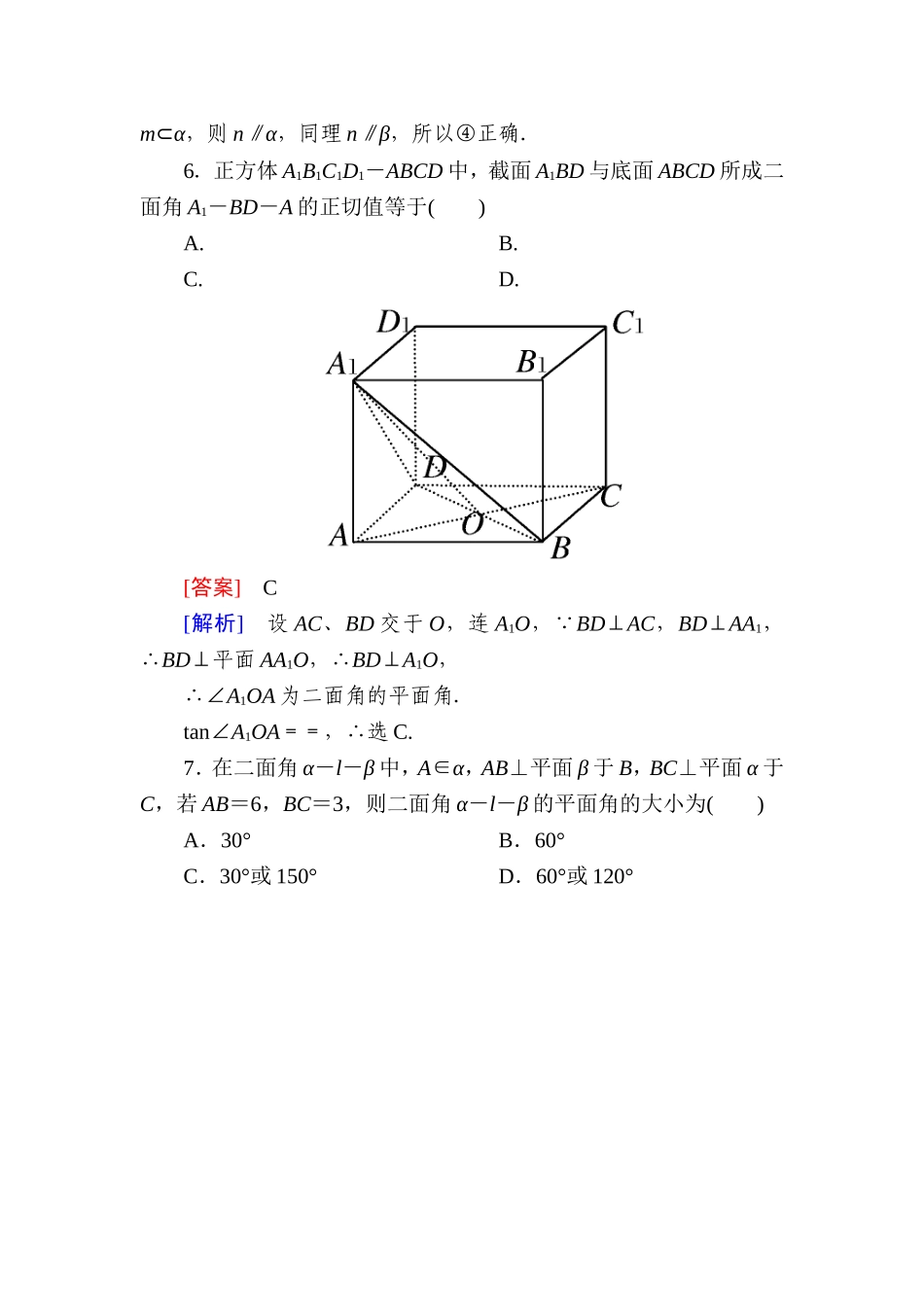
一、选择题1.下列命题中:①两个相交平面组成的图形叫做二面角;②异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角相等或互补;③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成角的最小角;④二面角的大小与其平面角的顶点在棱上的位置没有关系,其中正确的是()A.①③B.②④C.③④D.①②[答案]B[解析]对①,显然混淆了平面与半平面的概念,是错误的;对②,由于a,b分别垂直于两个面,所以也垂直于二面角的棱,但由于异面直线所成的角为锐角(或直角),所以应是相等或互补,是正确的;对③,因为不垂直于棱,所以是错误的;④是正确的,故选B.[点评]根据二面角的相关概念进行分析判定.2.以下三个命题中,正确的命题有()①一个二面角的平面角只有一个;②二面角的棱垂直于这个二面角的平面角所在的平面;③分别在二面角的两个半平面内,且垂直于棱的两直线所成的角等于二面角的大小A.0个B.1个C.2个D.3个[答案]B[解析]仅②正确.3.正方体ABCD-A1B1C1D1的六个面中,与平面BC1垂直的面的个数是()A.1B.2C.3D.4[答案]D[解析]与平面BC1垂直的面有:平面AC,平面A1C1,平面AB1,平面CD1.4.自二面角内任意一点分别向两个面引垂线,则两垂线的夹角与二面角的平面角的关系是()A.相等B.互补C.互余D.无法确定[答案]B[解析]如图,BD、CD为AB、AC所在平面与α、β的交线,则∠BDC为二面角α-l-β的平面角.且∠ABD=∠ACD=90°,∴∠A+∠BDC=180°.5.已知α,β是平面,m、n是直线,给出下列表述:①若m⊥α,m⊂β,则α⊥β;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;③如果m⊂α,n⊄α,m,n是异面直线,那么n与α相交;④若α∩β=m,n∥m,且n⊄α,n⊄β,则n∥α且n∥β.其中表述正确的个数是()A.1B.2C.3D.4[答案]B[解析]①是平面与平面垂直的判定定理,所以①正确;②中,m,n不一定是相交直线,不符合两个平面平行的判定定理,所以②不正确;③中,还可能n∥α,所以③不正确;④中,由于n∥m,n⊄α,m⊂α,则n∥α,同理n∥β,所以④正确.6.正方体A1B1C1D1-ABCD中,截面A1BD与底面ABCD所成二面角A1-BD-A的正切值等于()A.B.C.D.[答案]C[解析]设AC、BD交于O,连A1O, BD⊥AC,BD⊥AA1,∴BD⊥平面AA1O,∴BD⊥A1O,∴∠A1OA为二面角的平面角.tan∠A1OA==,∴选C.7.在二面角α-l-β中,A∈α,AB⊥平面β于B,BC⊥平面α于C,若AB=6,BC=3,则二面角α-l-β的...