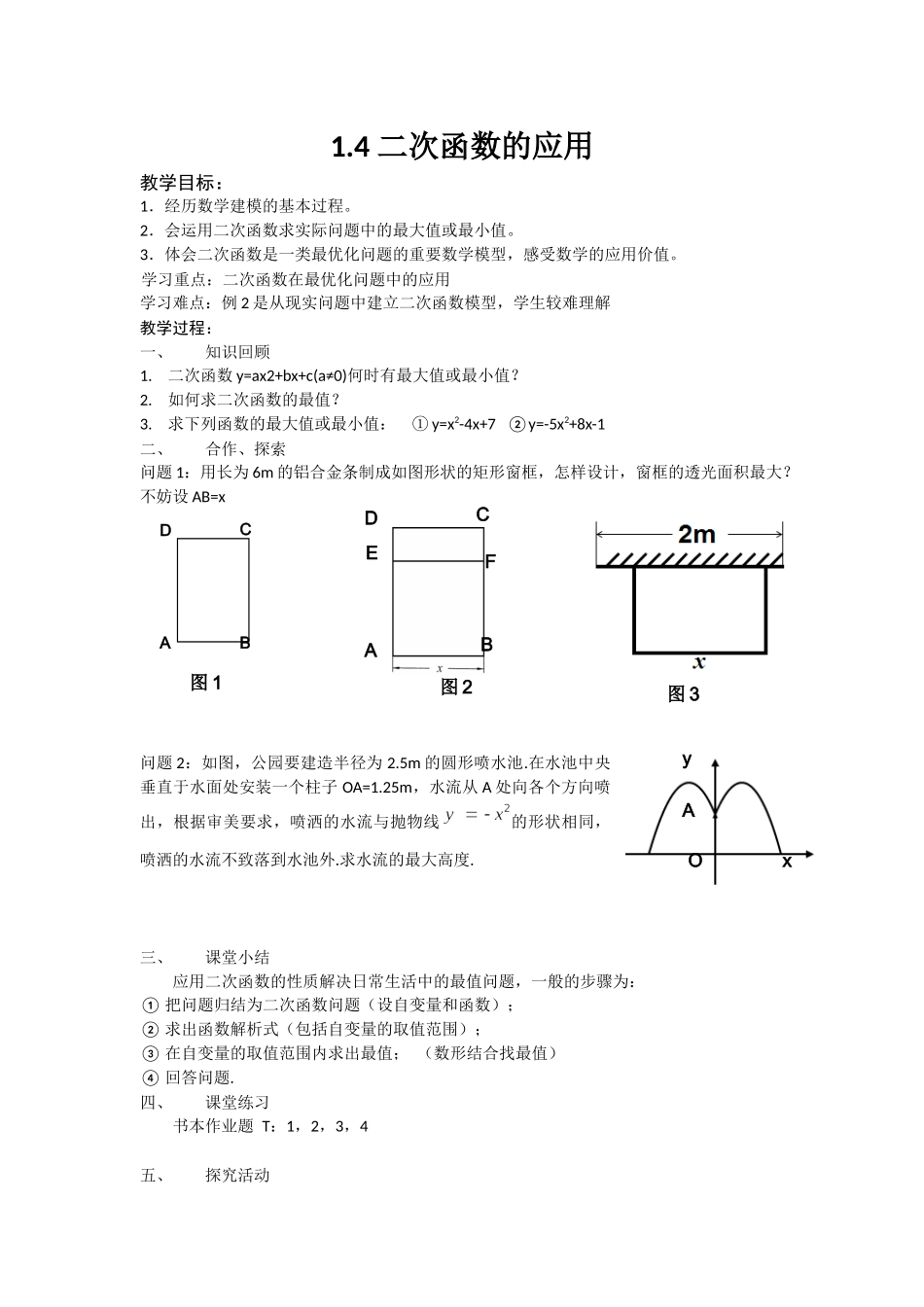
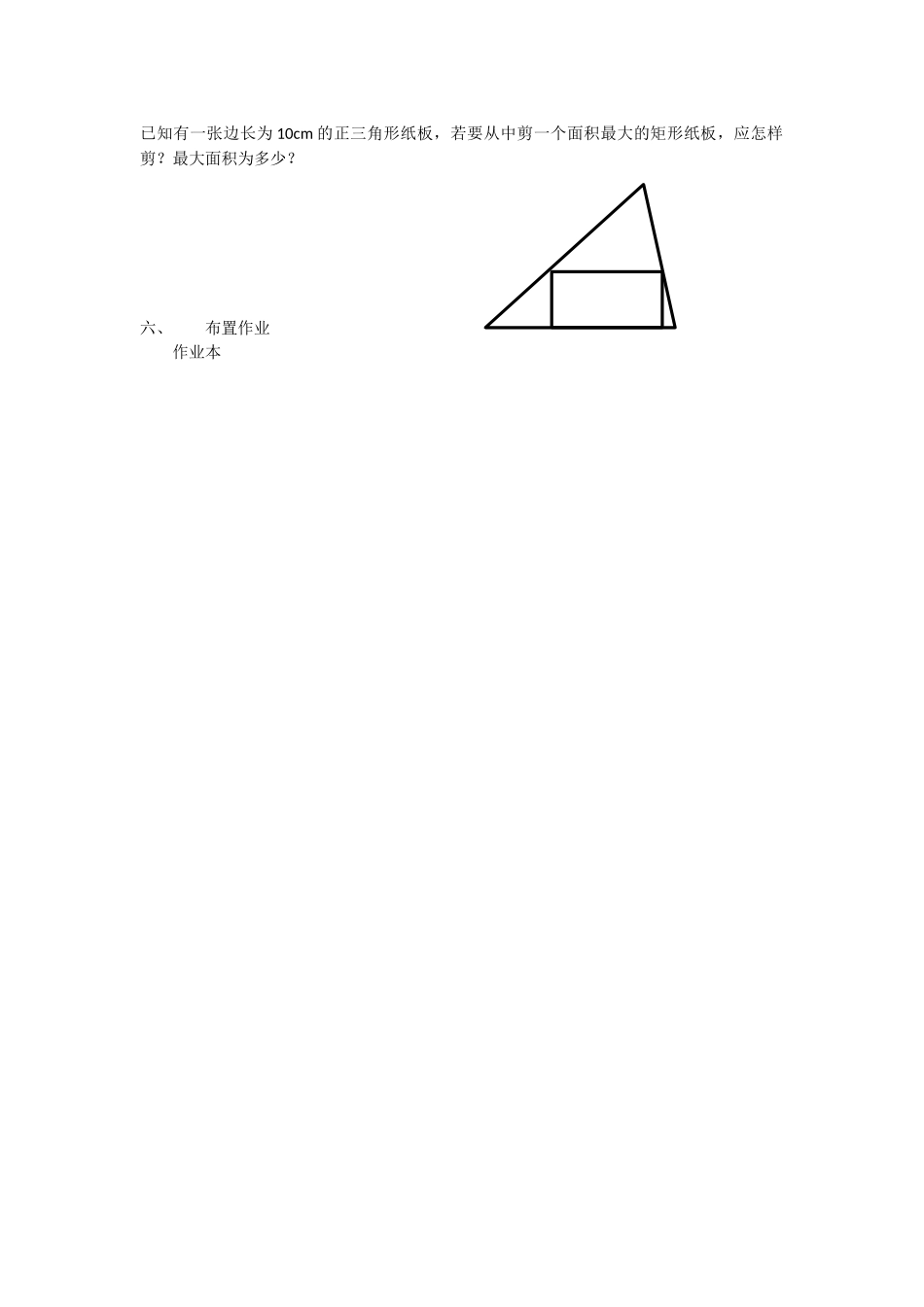
1.4二次函数的应用教学目标:1.经历数学建模的基本过程。2.会运用二次函数求实际问题中的最大值或最小值。3.体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值。学习重点:二次函数在最优化问题中的应用学习难点:例2是从现实问题中建立二次函数模型,学生较难理解教学过程:一、知识回顾1.二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?2.如何求二次函数的最值?3.求下列函数的最大值或最小值:①y=x2-4x+7②y=-5x2+8x-1二、合作、探索问题1:用长为6m的铝合金条制成如图形状的矩形窗框,怎样设计,窗框的透光面积最大?不妨设AB=x问题2:如图,公园要建造半径为2.5m的圆形喷水池.在水池中央垂直于水面处安装一个柱子OA=1.25m,水流从A处向各个方向喷出,根据审美要求,喷洒的水流与抛物线的形状相同,喷洒的水流不致落到水池外.求水流的最大高度.三、课堂小结应用二次函数的性质解决日常生活中的最值问题,一般的步骤为:①把问题归结为二次函数问题(设自变量和函数);②求出函数解析式(包括自变量的取值范围);③在自变量的取值范围内求出最值;(数形结合找最值)④回答问题.四、课堂练习书本作业题T:1,2,3,4五、探究活动DCBAED图2FCBA图1图3yxOA已知有一张边长为10cm的正三角形纸板,若要从中剪一个面积最大的矩形纸板,应怎样剪?最大面积为多少?六、布置作业作业本