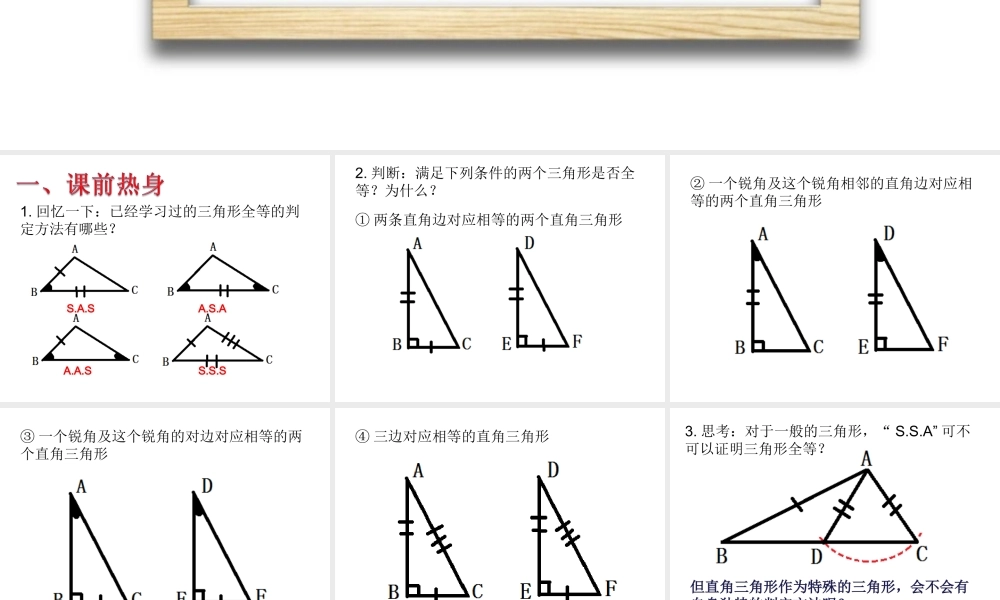
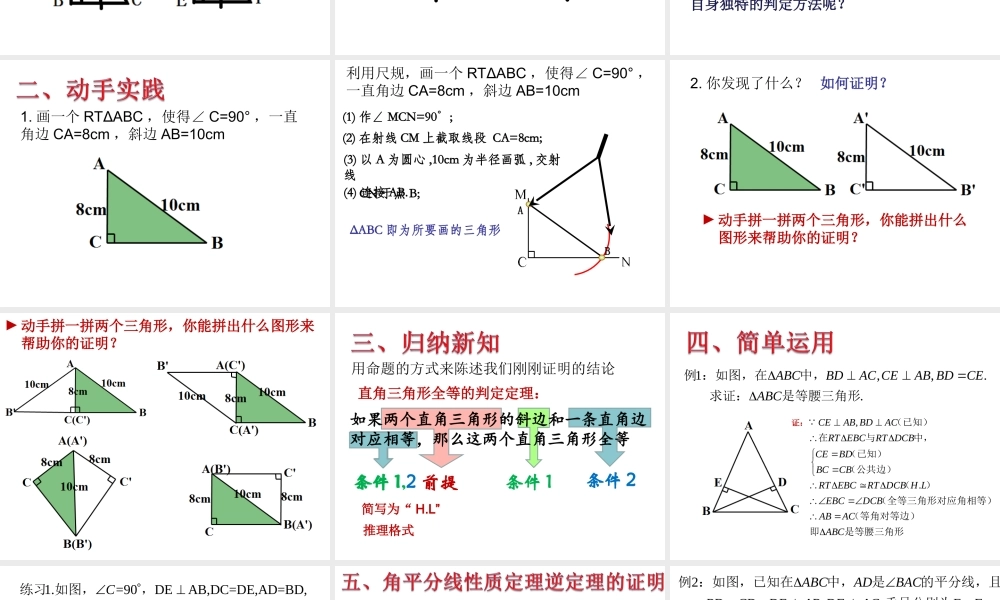
19.7直角三角形全等的判定1.回忆一下:已经学习过的三角形全等的判定方法有哪些?S.A.SA.S.AA.A.SS.S.S2.判断:满足下列条件的两个三角形是否全等?为什么?①两条直角边对应相等的两个直角三角形②一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形③一个锐角及这个锐角的对边对应相等的两个直角三角形④三边对应相等的直角三角形3.思考:对于一般的三角形,“S.S.A”可不可以证明三角形全等?但直角三角形作为特殊的三角形,会不会有自身独特的判定方法呢?1.画一个RTΔABC,使得∠C=90°,一直角边CA=8cm,斜边AB=10cm(1)作∠MCN=90°;(2)在射线CM上截取线段CA=8cm;(3)以A为圆心,10cm为半径画弧,交射线CN于点B;(4)连接AB.AB利用尺规,画一个RTΔABC,使得∠C=90°,一直角边CA=8cm,斜边AB=10cmΔABC即为所要画的三角形2.你发现了什么?如何证明?►动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?►动手拼一拼两个三角形,你能拼出什么图形来帮助你的证明?条件1,2用命题的方式来陈述我们刚刚证明的结论如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等前提条件1条件1条件2直角三角形全等的判定定理:简写为“H.L”推理格式1,,..ABCBDACCEABBDCEABC例:如图,在中,求证:是等腰三角形,.CEABBDACRTEBCRTDCBCEBDBCCBRTEBCRTDCBHLEBCDCBABACABC(已知)在与中,(已知)(公共边)()(全等三角形对应角相等)(等角对等边)即是等腰三角形证:1.=90DEAB,DC=DE,AD=BD,C练习如图,,图中有几对全等三角形?求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.OABQDE,,,QDOAQEOBDEQDQE已知:如图,垂足分别为,且,求证:点Q在AOB的平分线上2,,,ABCADBACBDCDDEABDFACEFBECF例:如图,已知在中,是的平分线,且,垂足分别为、试说明一般三角形全等的判定S.A.SA.S.AA.A.SS.S.S直角三角形全等的判定S.A.SA.S.AA.A.SH.L灵活运用各种方法证明直角三角形全等,,//,,CEABDFABACBDACBD如图,且求证:CE=DF1:还需什么条件才能证明结论?,,//,,CEABDFABACBDACBD如图,且求证:CE=DF变式1:还需什么条件才能用H.L证明结论?,,//,,CEABDFABACBDACBD如图,且求证:CE=DF变式2:还需什么条件才能用H.L证明结论?还需什么条件才能证明结论?,,,,CEABDFABAEBFACBD如图,且求证:CD平分EF变式3:1.图中有哪些全等三角形?2.改变部分条件和结论是否仍然成立?3.在ΔACE向右平移的过程中,平分与全等的结论是否始终成立?进一步: