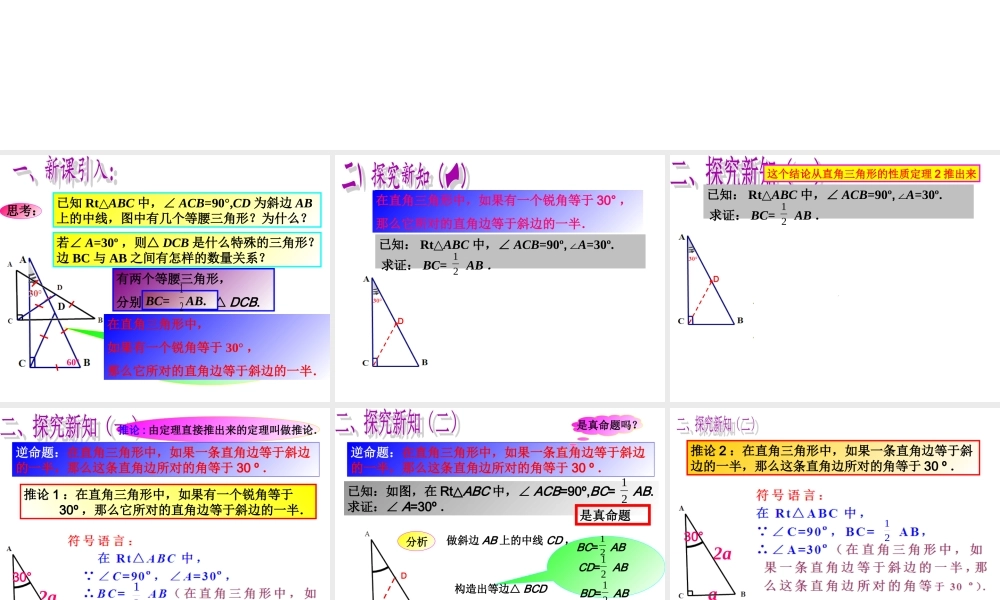
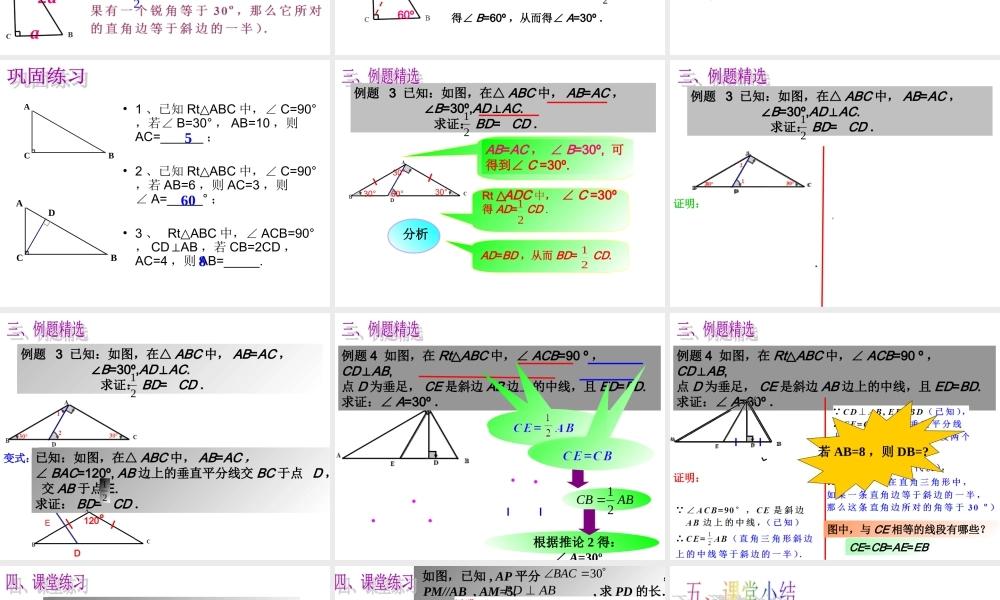
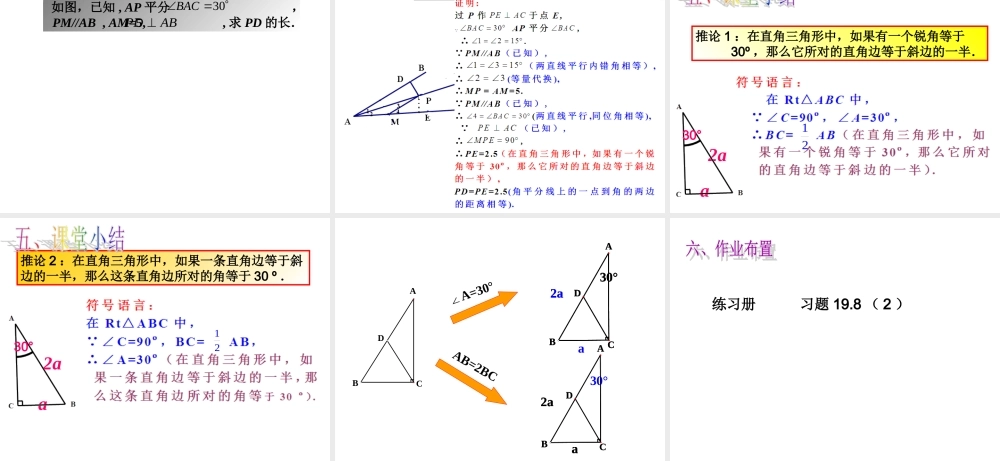
思考:已知Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线,图中有几个等腰三角形?为什么?有两个等腰三角形,分别是△ACD和△DCB.“直角三角形斜边上的中线等于斜边的一半”,即CD=AD=BD=AB.21若∠A=30º,则△DCB是什么特殊的三角形?边BC与AB之间有怎样的数量关系?在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.BC=AB.2160°在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.已知:Rt△ABC中,∠ACB=90º,∠A=30º.求证:BC=AB.21DABABAB已知:RtABC△中,∠ACB=90º,∠A=30º.求证:BC=AB.21D这个结论从直角三角形的性质定理2推出来推论:由定理直接推出来的定理叫做推论.以上命题的证明,是从直角三角形的性质定理2推出来的定理,把它称为直角三角形性质定理2的推论.推论1:在直角三角形中,如果有一个锐角等于30º,那么它所对的直角边等于斜边的一半.21逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30º.a2a30°21BC=AB21CD=AB21BD=AB逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30º.已知:如图,在Rt△ABC中,∠ACB=90º,BC=AB.求证:∠A=30º.21D分析做斜边AB上的中线CD,构造出等边△BCD得∠B=60º,从而得∠A=30º.是真命题吗?是真命题60º推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30º.21a2a30°•1、已知RtABC△中,∠C=90°,若∠B=30°,AB=10,则AC=______;•2、已知RtABC△中,∠C=90°,若AB=6,则AC=3,则∠A=_____°;•3、RtABC△中,∠ACB=90°,CDAB⊥,若CB=2CD,AC=4,则AB=_____.CBADCBA5608例题3已知:如图,在△ABC中,AB=AC,∠B=30º,AD⊥AC.求证:BD=CD.2130°30°60°AD=BD,从而BD=CD.2130°Rt△ADC中,∠C=30º得AD=CD.21AB=AC,∠B=30º,可得到∠C=30º.分析例题3已知:如图,在△ABC中,AB=AC,∠B=30º,AD⊥AC.求证:BD=CD.21证明:例题3已知:如图,在△ABC中,AB=AC,∠B=30º,AD⊥AC.求证:BD=CD.21变式:E已知:如图,在△ABC中,AB=AC,∠BAC=120º,AB边上的垂直平分线交BC于点D,交AB于点E.求证:BD=CD.21120°D例题4如图,在Rt△ABC中,∠ACB=90º,CD⊥AB,点D为垂足,CE是斜边AB边上的中线,且ED=BD.求证:∠A=30º.ABCB21根据推论2得:∠A=30º例题4如图,在Rt△ABC中,∠ACB=90º,CD⊥AB,点D...