1.4.2 用空间向量研究距离、夹角问题（第2课时）（教学课件）-2023-2024学年高二数学同步精品课堂（人教A版2019选择性必修第一册）.pptxVIP免费

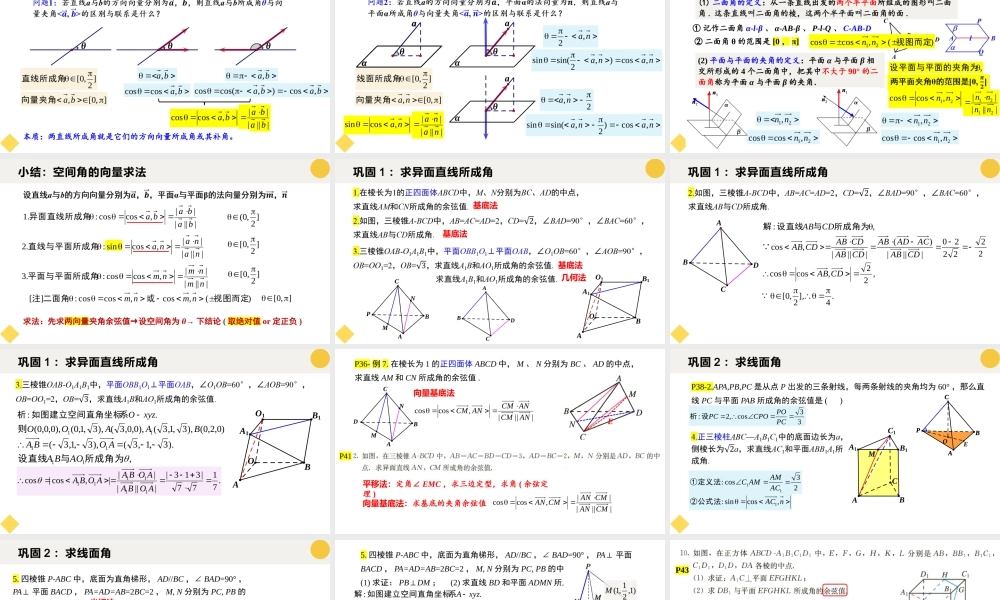
选修一《第一章空间向量与立体几何》1.4.2用空间向量研究距离、夹角问题第2课时用空间向量研究夹角问题空间角的向量求法——①线线角θθθba,ba,ba,coscosbaba,cos),cos(cos]2,0[直线所成角],0[,ba向量夹角ba,coscos||||||baba判断：两直线所成角就是它们的方向向量所成角。本质：两直线所成角就是它们的方向向量所成角或其补角。空间角的向量求法——②线面角na,22,nanana,cos),2sin(sin]2,0[线面所成角],0[,na向量夹角na,cossin||||||nanaαaθαaθαaθαanana,cos)2,sin(sin空间角的向量求法——③面面角(1)二面角的定义：从一条直线出发的两个半平面所组成的图形叫二面角.这条直线叫二面角的棱，这两个半平面叫二面角的面.①记作二面角α-l-β、α-AB-β、P-l-Q、C-AB-D②二面角θ的范围是[0，π](2)平面与平面的夹角的定义：平面α与平面β相交所形成的4个二面角中，把其中不大于90°的二面角称为平面α与平面β的夹角．21,nn21,nn21,coscosnn21,coscosnn,设平面与平面的夹角为21,coscosnn||||||2121nnnn)(,coscos21视图而定nn小结：空间角的向量求法||||||,coscos:.1bababa异面直线所成角]2,0(||||||,cossin:.2nanana直线与平面所成角]2,0[||||||,coscos:.3nmnmnm平面与平面所成角)(,cos,coscos:][视图而定或二面角注nmnm]2,0[],0[求法：先求两向量夹角余弦值→设空间角为θ→下结论(取绝对值or定正负)巩固1：求异面直线所成角ABDCNMCPBAO1B1BOA1A基底法基底法基底法几何法巩固1：求异面直线所成角ABDC222220||||)(||||,cos,:CDABACADABCDABCDABCDABCDAB 所成角为与设直线解,22,coscosCDAB.4],2,0[巩固1：求异面直线所成角.:xyzO系如图建立空间直角坐标析)0,2,0(),3,1,3(),0,0,3(),3,1,0(),0,0,0(11BAAOO则).3,1,3(),3,1,3(11AOBA.7177|313||||||||,cos|cos111111AOBAAOBAAOBA,11所成角为与设直线AOBAO1B1BOA1AP41P36-例7.在棱长为1的正四面体ABCD中，M、N分别为BC、AD的中点，求直线AM和CN所成角的余...