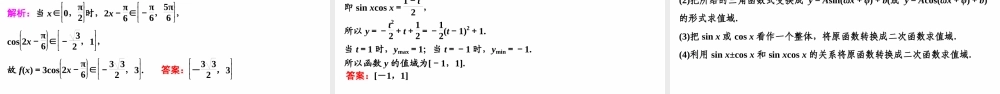【精品课件】第04讲 三角函数的图象与性质（第1课时 三角函数的单调性与最值）-备战2022年高考数学一轮复习精品课件（新高考地区专用）.pptxVIP免费

数学第4讲三角函数的单调性与最值高三一轮复习重难点题型求三角函数的单调区间(1)函数f(x)＝sin－2x＋π3的单调递减区间为________．(2)函数f(x)＝tan(2x＋π3)的单调递增区间是________．【解析】(1)f(x)＝sin－2x＋π3＝sin－2x－π3＝－sin2x－π3，由2kπ－π2≤2x－π3≤2kπ＋π2，k∈Z，得kπ－π12≤x≤kπ＋5π12，k∈Z.故所求函数的单调递减区间为kπ－π12，kπ＋5π12(k∈Z)．(2)由kπ－π2＜2x＋π3＜kπ＋π2(k∈Z)，得kπ2－5π12＜x＜kπ2＋π12(k∈Z)，所以函数f(x)＝tan2x＋π3的单调递增区间为kπ2－5π12，kπ2＋π12(k∈Z)．【答案】(1)kπ－π12，kπ＋5π12(k∈Z)(2)kπ2－5π12，kπ2＋π12(k∈Z)【引申探究】1．(变条件、变问法)若本例(1)f(x)变为：f(x)＝－cos－2x＋π3，求f(x)的单调递增区间．解：f(x)＝－cos－2x＋π3＝－cos2x－π3，欲求函数f(x)的单调递增区间，只需求y＝cos2x－π3的单调递减区间．由2kπ≤2x－π3≤2kπ＋π，k∈Z，得kπ＋π6≤x≤kπ＋2π3，k∈Z.故函数f(x)的单调递增区间为kπ＋π6，kπ＋2π3(k∈Z)．2．(变条件、变问法)本例(1)f(x)变为：f(x)＝sin2x－π3，试讨论f(x)在区间－π4，π4上的单调性．解：令z＝2x－π3，易知函数y＝sinz的单调递增区间是－π2＋2kπ，π2＋2kπ，k∈Z.由－π2＋2kπ≤2x－π3≤π2＋2kπ，得－π12＋kπ≤x≤5π12＋kπ，k∈Z.设A＝－π4，π4，B＝x|－π12＋kπ≤x≤5π12＋kπ，k∈Z，易知A∩B＝－π12，π4.所以，当x∈－π4，π4时，f(x)在区间－π12，π4上单调递增，又因为π4－－π4＝π2