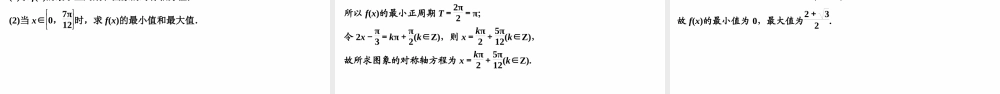【精品课件】第04讲 三角函数的图象与性质（第2课时 三角函数的周期性、奇偶性及对称性）-备战2022年高考数学一轮复习精品课件（新高考地区专用）.pptxVIP免费

数学三角函数的奇偶性、周期性、对称性高三一轮复习重难点题型√三角函数的周期性与奇偶性(1)(多选)已知函数f(x)＝sinx－π2(x∈R)，则下列结论正确的是()A．函数f(x)的最小正周期为2πB．函数f(x)在区间0，π2上是增函数C．函数f(x)的图象关于直线x＝0对称D．函数f(x)是奇函数√√(2)已知函数y＝2sin(ωx＋θ)(0＜θ＜π)为偶函数，其图象与直线y＝2的某两个交点的横坐标分别为x1，x2，|x2－x1|的最小值为π，则()A．ω＝2，θ＝π2B．ω＝12，θ＝π2C．ω＝12，θ＝π4D．ω＝2，θ＝π4√【解析】(1)由题意，可得f(x)＝－cosx，对于选项A，T＝2π1＝2π，所以选项A正确；对于选项B，y＝cosx在0，π2上是减函数，所以函数f(x)在区间0，π2上是增函数，所以选项B正确；对于选项C，f(－x)＝－cos(－x)＝－cosx＝f(x)，所以函数是偶函数，所以其图象关于直线x＝0对称，所以选项C正确；选项D错误．故选ABC.(2)因为函数y＝2sin(ωx＋θ)的最大值为2，且其图象与直线y＝2的某两个交点的横坐标分别为x1，x2，|x2－x1|的最小值为π，所以函数y＝2sin(ωx＋θ)的最小正周期是π.由2πω＝π得ω＝2.因为函数y＝2sin(ωx＋θ)为偶函数，所以θ＝π2＋kπ，k∈Z.又0＜θ＜π，所以θ＝π2，故选A.(1)奇偶性的判断方法：三角函数中奇函数一般可化为y＝Asinωx或y＝Atanωx的形式，而偶函数一般可化为y＝Acosωx＋b的形式．(2)周期的计算方法：利用函数y＝Asin(ωx＋φ)(ω>0)，y＝Acos(ωx＋φ)(ω＞0)的最小正周期为2πω，函数y＝Atan(ωx＋φ)(ω＞0)的最小正周期为πω求解．1．(多选)下列函数中，最小正周期为π的是()A．y＝cos|2x|B．y＝|cosx|C．y＝cos2x＋π6D．y＝tan2x－π4√√√解析：A项，y＝cos|2x|＝cos2x，最小正周期为π；B项，由图象知y＝|cosx|的最小正周期为π；C项，y＝cos2x＋π6的最小正周期T＝2π2＝π；D项，y＝tan2x－π4的最小正周期T＝π2.2．设函数f(x)＝sinωx＋φ－π4ω＞0，|φ|＜π2的最小正周期为π，且f(－x)＝f(x)，则()A．f(x)在0，π2上单调递增B．f(x)在－π2，π2上单调递减C．f(x)在0，π2上单调递减D．f(x)在－π2，π2上单调递增√解析：f(x)＝sinωx＋...