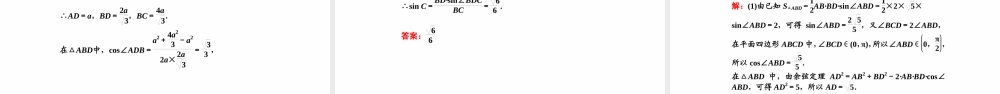数学第7讲解三角形应用举例及综合问题高三一轮复习重难点题型考点一解三角形的实际应用考向(一)测量距离问题[例1]如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为3003m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=60°,则P,Q两点间的距离为________m.[解析]由已知,得∠QAB=∠PAB-∠PAQ=30°.又∠PBA=∠PBQ=60°,所以∠AQB=30°,所以AB=BQ.又PB为公共边,所以△PAB≌△PQB,所以PQ=PA.在Rt△PAB中,AP=AB·tan60°=900,故PQ=900,所以P,Q两点间的距离为900m.[答案]900[解题技法]测量距离问题的2个策略(1)选定或确定要创建的三角形,首先确定所求量所在的三角形,若其他量已知则直接求解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.考向(二)测量高度问题[例2]如图,为了测量河对岸电视塔CD的高度,小王在点A处测得塔顶D的仰角为30°,塔底C与A的连线同河岸成15°角,小王向前走了1200m到达M处,测得塔底C与M的连线同河岸成60°角,则电视塔CD的高度为________m.[解析]在△ACM中,∠MCA=60°-15°=45°,∠AMC=180°-60°=120°,由正弦定理得AMsin∠MCA=ACsin∠AMC,即120022=AC32,解得AC=6006(m).在△ACD中,因为tan∠DAC=DCAC=33,所以DC=6006×33=6002(m).[答案]6002[解题技法]高度也是两点之间的距离,其解法同测量水平面上两点间距离的方法是类似的,基本思想是把要求解的高度(某线段的长度)纳入到一个可解的三角形中,使用正、余弦定理或其他相关知识求出该高度.考向(三)测量角度问题[例3]游客从某旅游景区的景点A处至景点C处有两条线路.线路1是从A沿直线步行到C,线路2是先从A沿直线步行到景点B处,然后从B沿直线步行到C.现有甲、乙两位游客从A处同时出发匀速步行,甲的速度是乙的速度的119倍,甲走线路2,乙走线路1,最后他们同时到达C处.经测量,AB=1040m,BC=500m,则sin∠BAC等于________.[解析]依题意,设乙的速度为xm/s,则甲的速度为119xm/s,因为AB=1040m,BC=500m,所以ACx=1040+500119x,解得AC=1260m.在△ABC中,由余弦定理得,cos∠BAC=AB2+AC2-BC22AB·AC=10402+12602-50022×1040×1260=1213,所以sin∠BAC=1-cos2∠BAC=1-12132=513.[答案]513[解题技法]测量角度问题的基本思路测量角度...