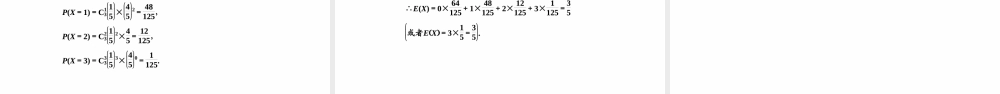数学第7讲离散型随机变量的均值与方差、正态分布高三一轮复习重难点题型考点一离散型随机变量的均值与方差[例1]为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为14,16;1小时以上且不超过2小时离开的概率分别为12,23;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ(单位:元),求ξ的分布列与数学期望E(ξ),方差D(ξ).[解](1)两人所付费用相同,相同的费用可能为0,40,80元,两人都付0元的概率为P1=14×16=124,两人都付40元的概率为P2=12×23=13,两人都付80元的概率为P3=1-14-12×1-16-23=14×16=124,故两人所付费用相同的概率为P=P1+P2+P3=124+13+124=512.(2)由题设甲、乙所付费用之和为ξ,ξ可能取值为0,40,80,120,160,则:P(ξ=0)=14×16=124,P(ξ=40)=14×23+12×16=14,P(ξ=80)=14×16+12×23+16×14=512,P(ξ=120)=12×16+14×23=14,P(ξ=160)=14×16=124.ξ的分布列为ξ04080120160P1241451214124E(ξ)=0×124+40×14+80×512+120×14+160×124=80.D(ξ)=(0-80)2×124+(40-80)2×14+(80-80)2×512+(120-80)2×14+(160-80)2×124=40003.[解题技法]求离散型随机变量ξ的均值与方差的步骤(1)理解ξ的意义,写出ξ可能的全部值.(2)求ξ取每个值的概率.(3)写出ξ的分布列.(4)由均值的定义求E(ξ).(5)由方差的定义求D(ξ).[跟踪训练]1.(2019·浙江高考)设0