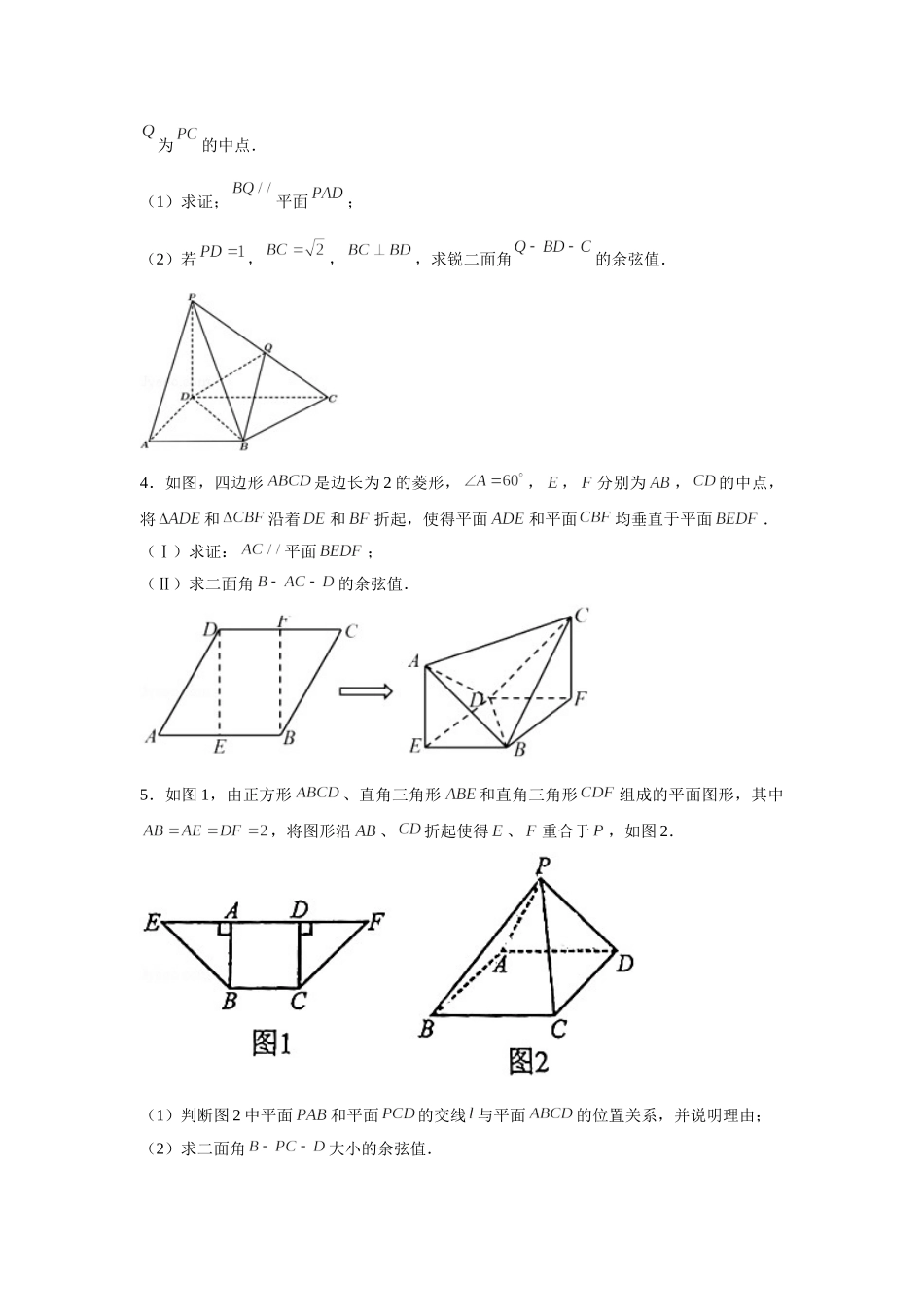
第八章立体几何专题训练(五)—二面角一.解答题1.如图,已知直四棱柱的底面为平行四边形,,,为棱的中点.(1)求证:平面;(2)求二面角的余弦值.2.如图,在四棱锥中,平面平面,是等边三角形,在直角梯形中,,,,,是棱的中点.(1)求证:平面;(2)设点在线段上,若平面与平面所成的锐二面角的余弦值为,求的长.3.已知在四棱锥中,平面,,,,为的中点.(1)求证;平面;(2)若,,,求锐二面角的余弦值.4.如图,四边形是边长为2的菱形,,,分别为,的中点,将和沿着和折起,使得平面和平面均垂直于平面.(Ⅰ)求证:平面;(Ⅱ)求二面角的余弦值.5.如图1,由正方形、直角三角形和直角三角形组成的平面图形,其中,将图形沿、折起使得、重合于,如图2.(1)判断图2中平面和平面的交线与平面的位置关系,并说明理由;(2)求二面角大小的余弦值.6.如图,在四棱锥中,底面是平行四边形,,,,,点是的中点.(1)求证:平面平面;(2)求二面角的余弦值.第八章立体几何专题训练(五)—二面角答案1.解:(1)证明:因为四边形为平行四边形,所以,又,,所以,所以.(2分)在直四棱柱中,易得,又,所以平面,所以.连接,因为,所以△,则,(4分)又,所以,所以,由直四棱柱的特征易知,所以.又,所以平面.(6分)(2)由(1)可知,以为坐标原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,则,0,,,2,,,,所以,,(8分)设平面的法向量为,,,则,令,则,即.(10分)由(1)可知平面的一个法向量为,所以,由图知二面角的平面角为锐角,所以其余弦值为.(12分)2.(1)证明:如图,作交于点,连接,,,又,,,且,即有四边形是平行四边形,得,平面平面,平面平面,,平面,平面,而平面,则平面平面,为等边三角形,为的中点,则,平面,平面平面,平面平面,平面,又,平面;(2)解:如图,设是的中点,在正中,,作,,由平面平面,可得平面,则平面,再以,方向为,轴正方向建立如图所示的空间直角坐标系,则,0,,,0,,,,,,0,,,0,,,,,.,,,,0,,设平面的法向量为,,,由,取,得,1,;点在线段上,设其坐标为,0,,其中,,0,,,,,设平面的法向量为,,,由,取,得,,.由题意,设平面与平面所成的锐二面角为,则,整理得或,,,0,,.3.(1)证明:取的中点为,分别连接,,又因为为的中点,所以,且又因为,,所以,,所以四边形是平行...