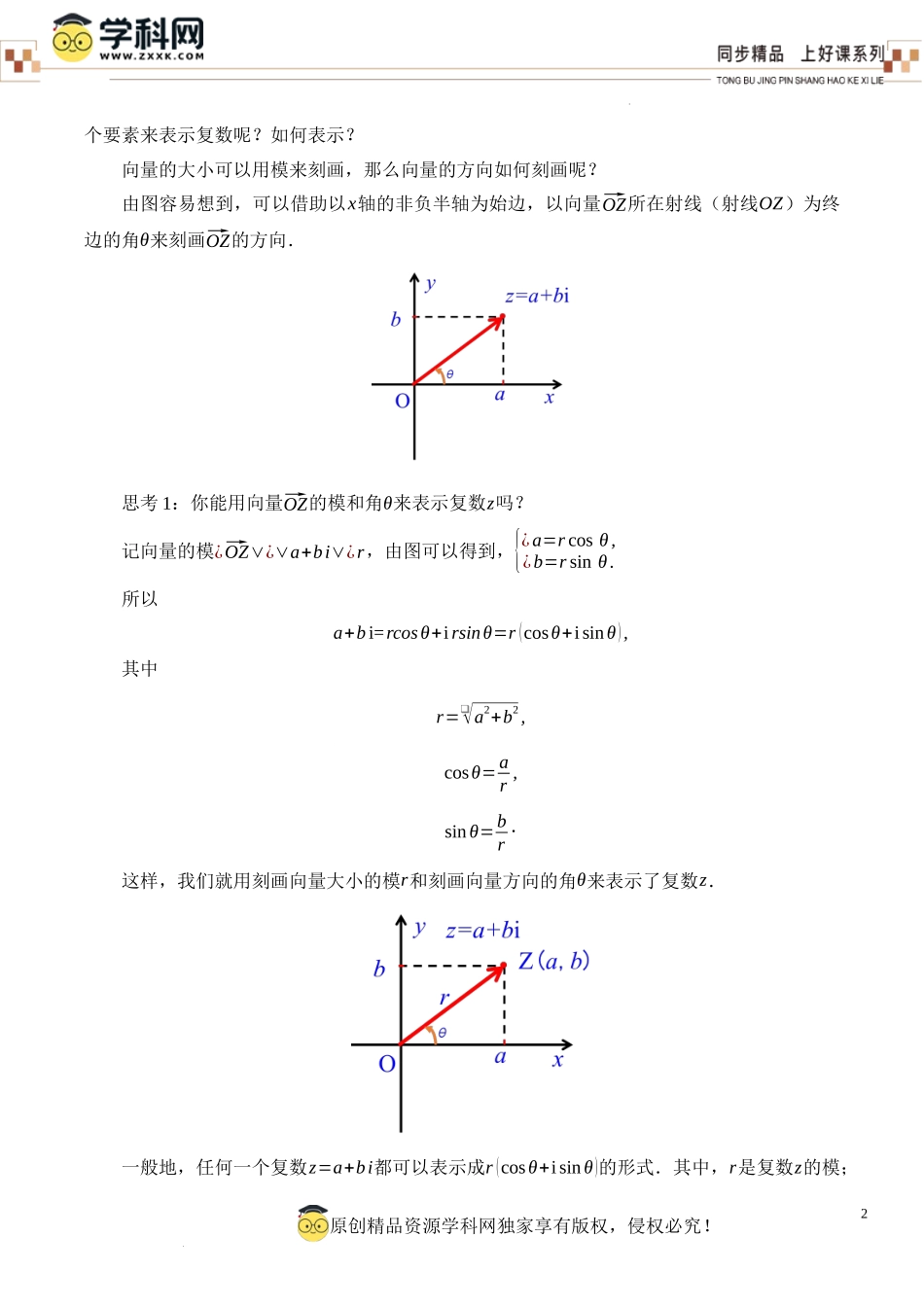
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司7.3.1*复数的三角表示式教学设计一、教学目标了解复数的三角表示.二、教学重难点1.教学重点:复数的三角表示式.2.教学难点:复数的三角表示.三、教学过程前面我们研究了复数a+bi,及其四则运算,本节研究复数的另一种重要表示——复数的三角表示.它可以帮助我们进一步认识复数,同时能给复数的运算带来便利.1、温故知新,奠定基础我们知道,复数可以用a+bi(a,b∈R)的形式来表示,复数a+bi与复平面内的点Z(a,b)是一一对应的,与平面向量⃗OZ=(a,b)也是一一对应的.借助复数的几何意义,复数能不能用其他形式来表示呢?2、引导探究,得出概念探究1:如图,复数z=a+bi与向量⃗OZ=(a,b)一一对应,复数z由向量⃗OZ的坐标(a,b)唯一确定.我们知道向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司个要素来表示复数呢?如何表示?向量的大小可以用模来刻画,那么向量的方向如何刻画呢?由图容易想到,可以借助以x轴的非负半轴为始边,以向量⃗OZ所在射线(射线OZ)为终边的角θ来刻画⃗OZ的方向.思考1:你能用向量⃗OZ的模和角θ来表示复数z吗?记向量的模¿⃗OZ∨¿∨a+bi∨¿r,由图可以得到,{¿a=rcosθ,¿b=rsinθ.所以a+bi=rcosθ+irsinθ=r(cosθ+isinθ),其中r=❑√a2+b2,cosθ=ar,sinθ=br⋅这样,我们就用刻画向量大小的模r和刻画向量方向的角θ来表示了复数z.一般地,任何一个复数z=a+bi都可以表示成r(cosθ+isinθ)的形式.其中,r是复数z的模;3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司θ是以x轴的非负半轴为始边,向量⃗OZ所在射线(射线OZ)为终边的角,叫做复数z=a+bi的辐角.r(cosθ+isinθ)叫做复数z=a+bi的三角表示式,简称三角形式.注:为了与三角形式区分开来,a+bi叫做复数的代数表示式,简称代数形式.辨析:1)任何一个不为零的复数的辐角有无限多个值,且这些值相差2π的整数倍.例如,复数i的辐角是π2+2kπ,其中k可以取任何整数.2)对于复数0,因为它对应着零向量,而零向量的方向是任意的,所以复数0的辐角也是任意的.3)在0⩽θ<2π范围内的辐角θ的值为辐角的主值.通常记作argz,即0⩽argz<2π.例如,argl=0,argi=π2,arg(−1)=π,arg(−i)=3π2.设计意图:让学生能够了解复数的三角形式,以及辐角...