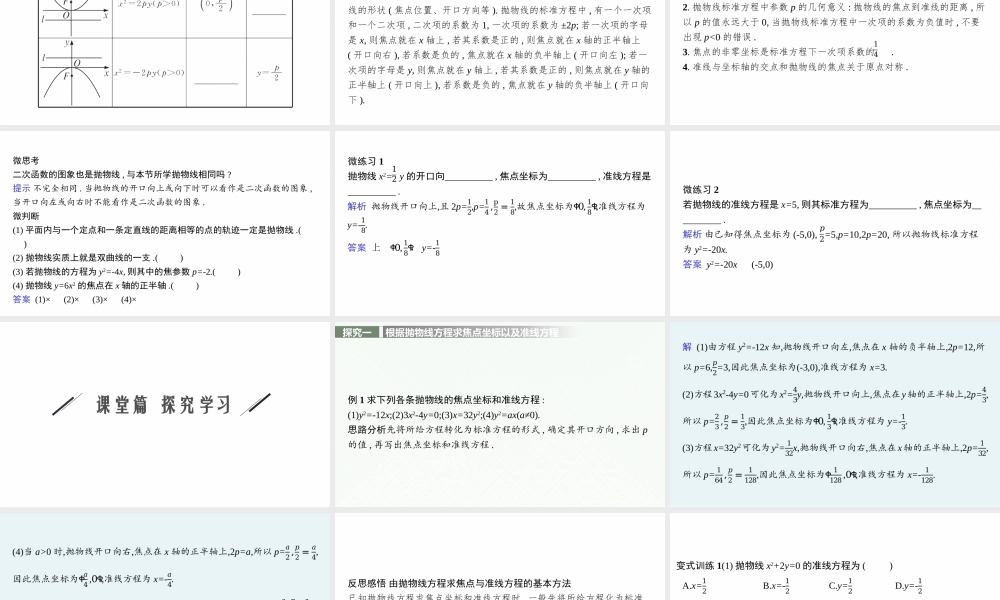
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI3.3.1抛物线及其标准方程第三章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释1.了解抛物线的定义、几何图形和标准方程.(数学抽象)2.体会数形结合思想在抛物线问题中的应用.(直观想象)3.会解决抛物线的简单应用问题.(数学建模)思维脉络课前篇自主预习[激趣诱思]我们把一根直尺固定在图板上直线l的位置,把一块三角尺的一条直角边紧靠着直尺的边缘,再把一条细绳的一端固定在三角尺的另一条直角边的一点A,取绳长等于点A到直角顶点C的长(即点A到直线l的距离),并且把绳子的另一端固定在图板上的一点F.用铅笔尖引着绳子,使点A到笔尖的一段绳子紧靠着三角尺,然后将三角尺沿着直尺上下滑动,笔尖就在图板上描出了一条曲线.这就是本节我们要学习的抛物线,这条曲线上的点有什么特征?[知识点拨]一、抛物线的定义1.我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.2.数学表达式:抛物线是点的集合P={M||MF|=d}.名师点析抛物线的定义实质可以归结为“一动二定一相等”:“一动”即一个动点,设为M;“二定”包括一个定点F,即抛物线的焦点,和一条定直线l,即抛物线的准线;一相等,即|MF|=d(d为M到准线l的距离).微思考定义中为什么要求直线l不经过点F?提示当直线l经过点F时,点的轨迹是过点F且垂直于直线l的一条直线,而不是抛物线.微练习1若动点P到点(3,0)的距离和它到直线x=-3的距离相等,则动点P的轨迹是()A.椭圆B.抛物线C.直线D.双曲线解析由抛物线定义知,动点轨迹为抛物线.答案B微练习2平面内到点A(2,3)和直线l:x+2y-8=0距离相等的点的轨迹是()A.直线B.抛物线C.椭圆D.圆解析A∈l,轨迹为过A且与l垂直的一条直线.答案A二、抛物线的标准方程名师点析1.要注意弄清抛物线四种形式的标准方程的特征及其对应抛物线的形状(焦点位置、开口方向等).抛物线的标准方程中,有一个一次项和一个二次项,二次项的系数为1,一次项的系数为±2p;若一次项的字母是x,则焦点就在x轴上,若其系数是正的,则焦点就在x轴的正半轴上(开口向右),若系数是负的,焦点就在x轴的负半轴上(开口向左);若一次项的字母是y,则焦点就在y轴上,若其系数是正的,则焦点就在y轴的正半轴上(开口向上),若系数是负的,焦点就在y轴的负半轴上(开口向下).2.抛物线标准方程中参数p的几何意义:抛物线的焦点到准线的距离,所以p的值永远大于0,当抛物线标准方程中一次项的系数为负值时,不...