高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI2.1.2基本不等式第2章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.理解基本不等式a2+b2≥2ab,(a≥0,b≥0).(数学抽象)2.结合具体实例,能用基本不等式解决简单的求最大值或最小值的问题.(数学运算)a+b2≥ξab课前篇自主预习情境导入某金店有一座天平,由于左右两臂长略有不等,所以直接称重不准确.有一个顾客要买一串金项链,店主分别把项链放于左右两盘各称一次,得到两个不同的质量a和b,然后就把两次称得的质量的算术平均数作为项链的质量来计算.顾客对这个质量的真实性提出了质疑,那么这样计算的质量相对于原来的真实质量到底是大了还是小了呢?𝑎+𝑏2知识梳理知识点:基本不等式1.定理:对任意a,b∈R,必有a2+b2≥2ab,当且仅当a=b时等号成立.2.推论:对任意a,b≥0,必有,当且仅当a=b时等号成立.𝑎+𝑏2≥ξ𝑎𝑏算术平均数几何平均数上述定理和推论中的不等式通常称为基本不等式.名师点析基本不等式定理和推论的区别与联系基本不等式a2+b2≥2ab适用范围a,b∈Ra≥0,b≥0文字叙述两数的平方和不小于它们积的2倍两个非负数的算术平均数不小于它们的几何平均数“=”成立的条件a=ba=b𝑎+𝑏2≥ξ𝑎𝑏微思考(1)基本不等式中的定理和推论之间有怎样的联系?(2)当a>0,b>0时,由a2+b2≥2ab你能得到哪些变形式?提示(1)当a≥0,b≥0时,用ξ𝑎,ξ𝑏分别代替定理中的a,b即可得到推论.(2)将不等式的两边分别同时除以a并且移项后可以得到a≥2b-𝑏2𝑎,同理将不等式的两边分别同时除以b并且移项后可以得到b≥2a-𝑎2𝑏,将上述两式左右两边分别相加后可得𝑏2𝑎+𝑎2𝑏≥a+b(当且仅当a=b时等号成立).课堂篇探究学习探究一对基本不等式的理解例1(多选题)设a>0,b>0,下列不等式恒成立的是()A.a2+1>aB.ቀ𝑎+1𝑎ቁቀ𝑏+1𝑏ቁ≥4C.(a+b)ቀ1𝑎+1𝑏ቁ≥4D.a-1+4𝑎-1≥4答案ABC解析A中,由于a2+1-a=ቀ𝑎-12ቁ2+34>0,∴a2+1>a,故A正确;B中,由于a+1𝑎≥2,b+1𝑏≥2,∴(a+1𝑎)(b+1𝑏)≥4,当且仅当a=b=1时等号成立,故B正确;C中,由于a+b≥2ξ𝑎𝑏,1𝑎+1𝑏≥2ට1𝑎𝑏,∴(a+b)(1𝑎+1𝑏)≥4,当且仅当a=b时等号成立,故C正确;D中,当0
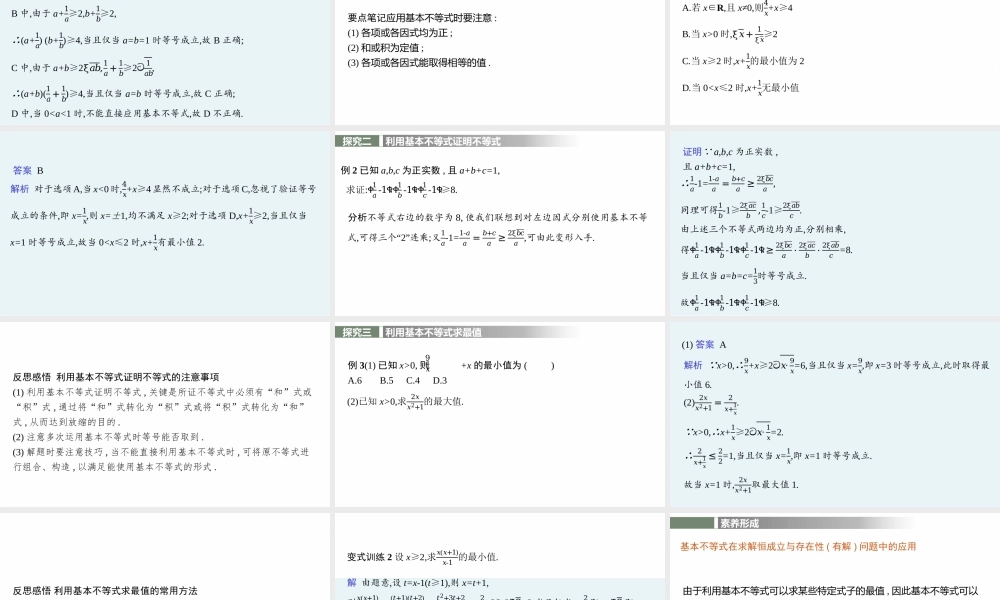
0时,ξ𝑥+1ξ𝑥≥2C.当x≥2时,x+1𝑥的最小值为2D.当0