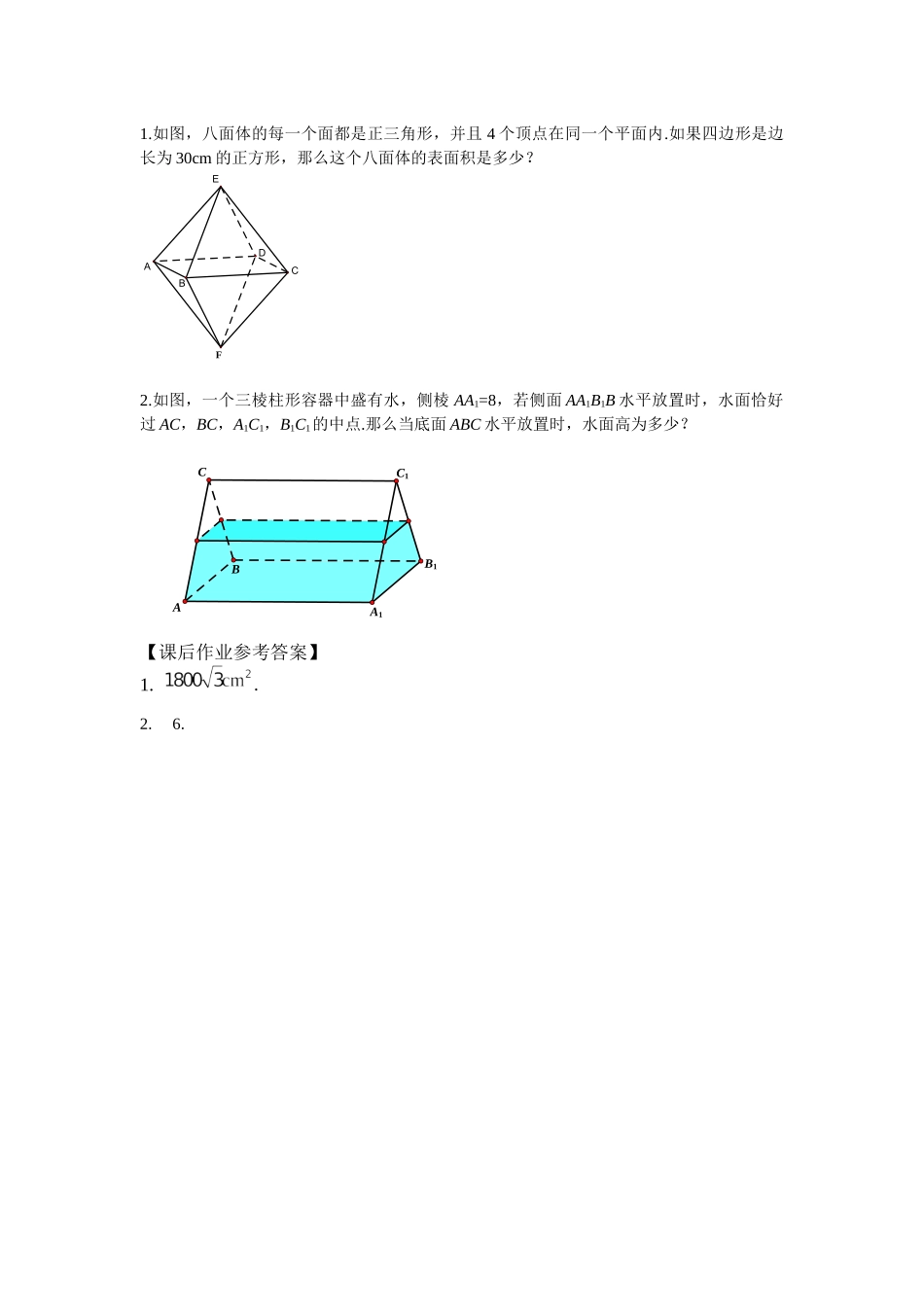
《棱柱、棱锥、棱台的表面积和体积》学习任务单【学习目标】1.通过对棱柱、棱锥、棱台的研究,掌握它们的表面积与体积的公式及求法;2.掌握与多面体相关的简单几何体的表面积与体积的求法,并能解决一些有关的实际问题;3.通过学习培养转化、类比、一般化与特殊化等思想方法;提高逻辑推理、直观想象等素养和空间想象等能力.【课上任务】1.前面我们学习了棱柱、棱锥、棱台的概念,大家还记得它们的结构特征吗?2.思考:棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算他们的表面积?3.思考:同一摞书,当改变摆放书的形式时,这摞书的总体积是否会改变?由此能得到有关体积的什么结论?4.如果棱柱的底面面积是S,高是h,那么棱柱的体积公式是什么?5.探究棱锥与同底等高的棱柱体积之间的关系?如果棱锥的底面面积为S,高为h,则该棱锥的体积公式是什么?6.棱台的体积公式怎么推导?7.观察棱柱、棱锥、棱台的体积公式:它们之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?8.总结下求空间几何体体积常用的方法?【学习疑问】(可选)9.哪段文字没看明白?10.哪个环节没弄清楚?11.有什么困惑?12.您想向同伴提出什么问题?13.您想向老师提出什么问题?14.没看明白的文字,用自己的话怎么说?15.本节课有几个环节,环节之间的联系和顺序?16.同伴提出的问题,您怎么解决?【课后作业】1.如图,八面体的每一个面都是正三角形,并且4个顶点在同一个平面内.如果四边形是边长为30cm的正方形,那么这个八面体的表面积是多少?FBDCAE2.如图,一个三棱柱形容器中盛有水,侧棱AA1=8,若侧面AA1B1B水平放置时,水面恰好过AC,BC,A1C1,B1C1的中点.那么当底面ABC水平放置时,水面高为多少?C1B1CBAA1【课后作业参考答案】1..2.6.