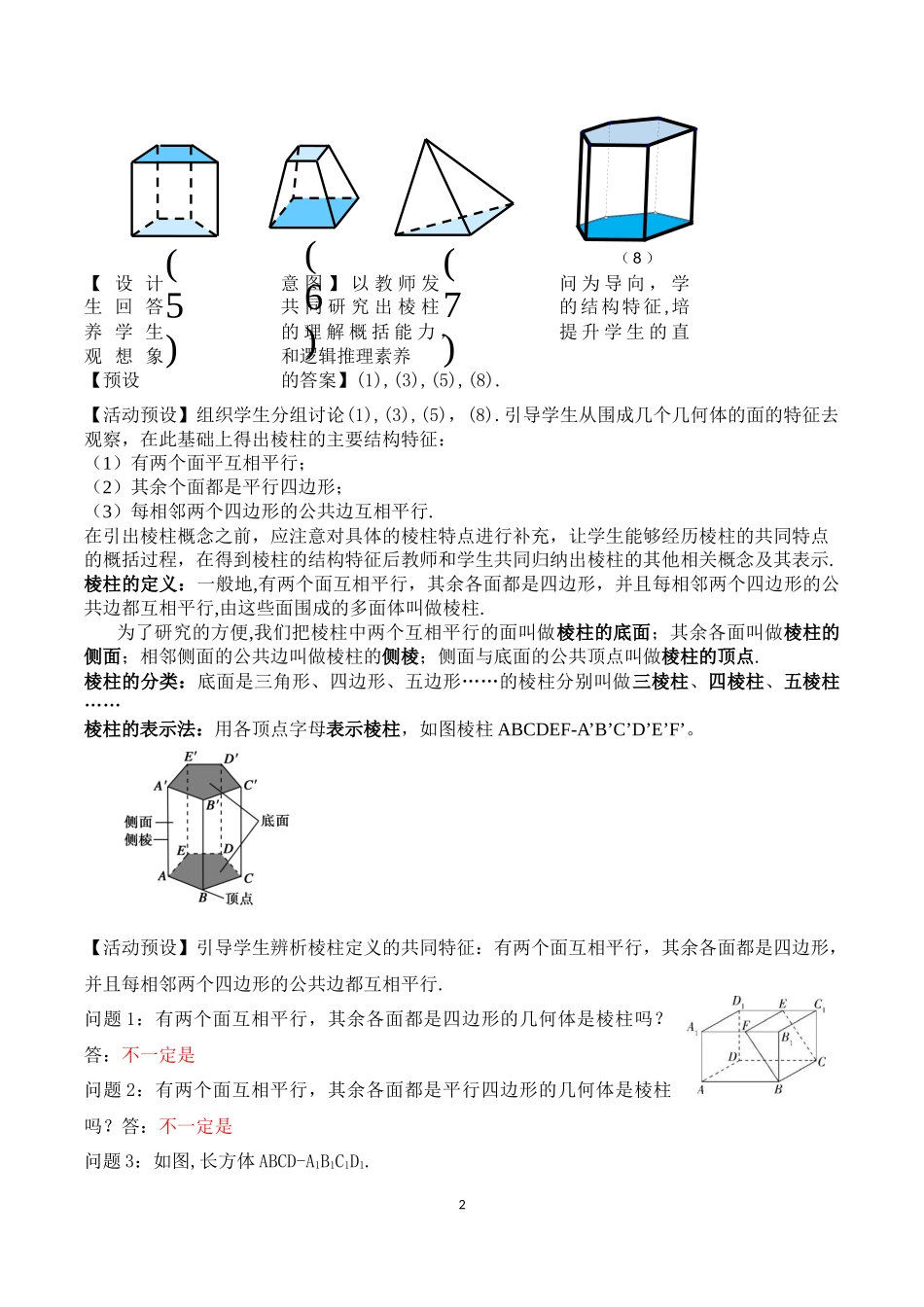
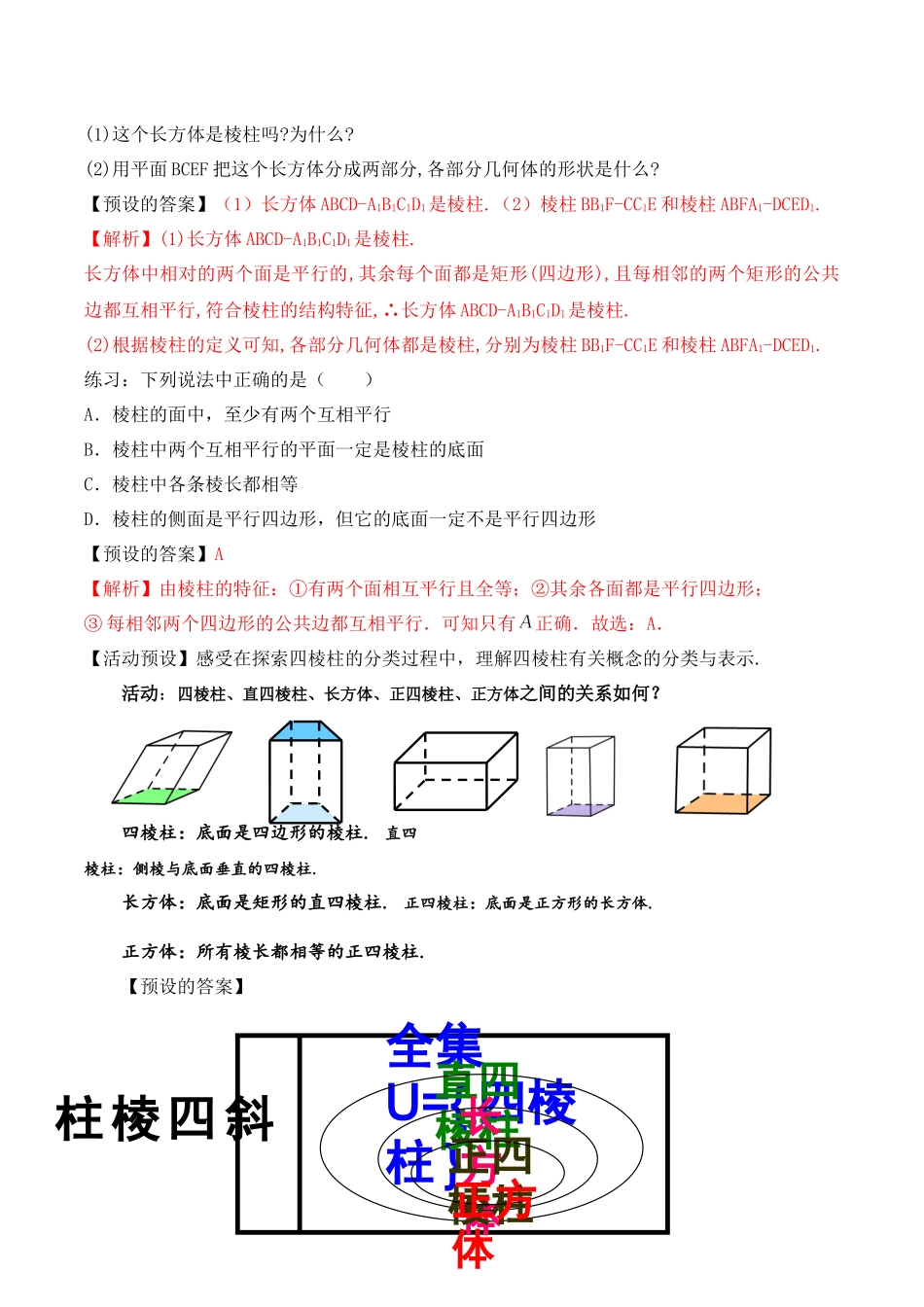
18.1.1基本立体图形(第一课时)(人教A版普通高中教科书数学必修第二册第八章)第二实验学校廖金龙一、教学目标1.通过计算机模拟或者利用实物概括出棱柱、棱锥、棱台的几何结构特征;2.能用数学语言概述棱柱、棱锥、棱台的结构特征;3.能表示有关几何体以及进行棱柱、棱锥、棱台的分类。4.通过对棱柱、棱锥、棱台的学习,培养学生数学抽象、逻辑推理、直观想象等数学素养。二、教学重难点1.让学生观察大量空间实物及计算机模型,进而概括出棱柱、棱锥、棱台的结构特征;2.会进行多面体的分类,表示;以及相关的底面,侧面,侧棱,顶点等概念的理解。三、教学过程8.1.1.多面体、旋转体的概念的形成我们生活中除了存在大量的平面图形:三角形,正方形,矩形,菱形,梯形,圆,扇形等,在我们周围还存在着很多的物体,它们都占据着空间的一部分.阅读课本以及通过计算机模拟生活中的一些物体,让学生小组合作完成以下问题师:在初中我们都学习过那些几何图形呢,空间几何图形都有哪些?生:三角形、正方形、长方形、平行四边形、长方体、正方体、棱锥、圆锥、圆柱等师:进入高中我们将继续深入研究空间几何图形.【讨论】下列物体(教材第97页图8.1-1)具有怎样的形状?在日常生活中,我们把这些物体的形状叫做什么?如何描述它们的形状?【互动】学生讨论交流回答,教师指导,并且给出多面体、旋转体的概念.【设计意图】用问题情景进行承上启下,引入课题,激发学生的学习兴趣空间几何体的定义:如果只考虑物体的形状和大小,而不考虑其它因素,那么这些由物体抽象出来的空间图形就叫做空间几何体。多面体的定义:由若干平面多边形围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点.旋转体的定义:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.【设计意图】以教师发问,学生回答共同研究出棱柱的结构特征培养学生的理解概括能力,提升学生的直观想象和逻辑推理素养8.1.2棱柱的结构特征【活动预设】引导学生归纳概括出问题的共同特征,得出棱柱的定义。师:观察下面的几何体,哪些是棱柱?(2)(3)(4)(1)2【设计意图】以教师发问为导向,学生回答共同研究出棱柱的结构特征,培养学生的理解概括能力,提升学生的直观想象和逻辑推理素养【预设的答案】(1),(3),(5),(8).【活动预设】组织学生分组讨论(1),(3),(5),(8).引导学生从围成几个...