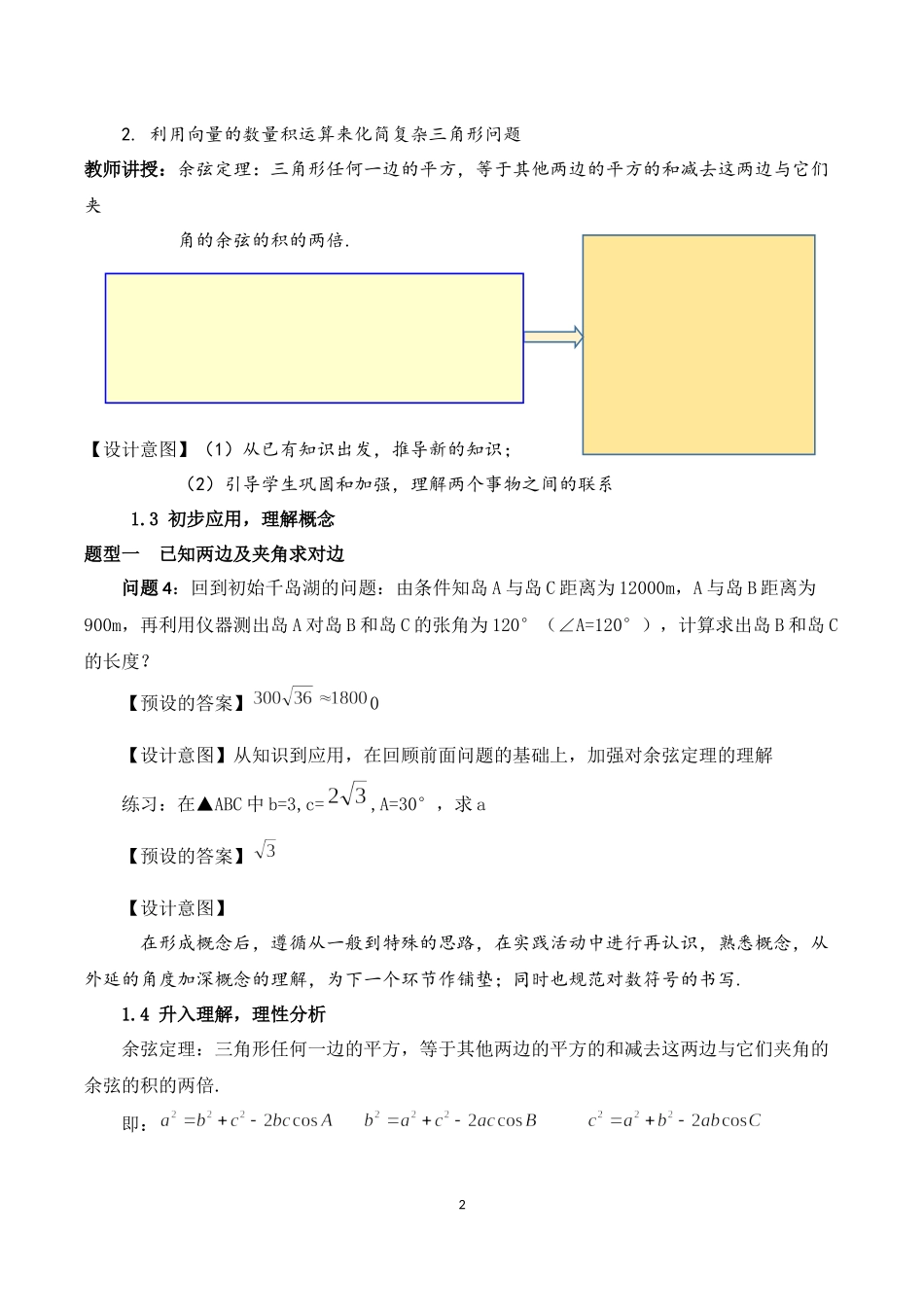
16.4.3平面向量的应用(第一课时)余弦定理(人教A版普通高中教科书数学必修第二册第六章)翠园中学雷小明一、教学目标1.借助向量的运算,推导余弦定理;2.掌握余弦定理的几种变形公式及应用;3.能利用余弦定理求解三角形的边、角等问题.二、教学重难点1.余弦定理变形公式及应用2.会利用公式解三角形三、教学过程1.1创设情境,引发思考【实际情境】千岛湖位于杭州杭州到黄山之间,距离汉州129公里,黄山140公里,是这黄金旅游线上一颗璀璨的明珠,下图就是千岛湖的部分照片.问题1:现在千岛湖上又三座岛屿,岛A、岛B和岛C,其中AB之间的距离1200m,AC之间的距离900m,用测角器测得∠BAC之间的角度为120°,现在想知道BC之间的距离,用什么方法来计算?【设计意图】由实际问题出发,引出问题,引导学生思考.【数学情境】把上述问题数学化,让岛A、岛B和岛分别在▲ABC的三个顶点上,且AC=1200m,AB=900m,∠A=120°,要求边BC的长度?【设计意图】把实际问题转化为数学问题,初步让学生感受到数学建模的乐趣.追问:更一般化,如果知道三角形的两个邻边和夹角,怎样求对边?【活动预设】引导学生归纳概括出问题的共同特征,进一步提出数学建模思想.1.2探索新知,形成概念问题3:在一个三角形中,如果知道邻边和夹角,利用前面的向量知识,能不能求出对边?【活动预设】1.把平面向量的知识过度到三角形中来,学会知识迁移22.利用向量的数量积运算来化简复杂三角形问题教师讲授:余弦定理:三角形任何一边的平方,等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍.【设计意图】(1)从已有知识出发,推导新的知识;(2)引导学生巩固和加强,理解两个事物之间的联系1.3初步应用,理解概念题型一已知两边及夹角求对边问题4:回到初始千岛湖的问题:由条件知岛A与岛C距离为12000m,A与岛B距离为900m,再利用仪器测出岛A对岛B和岛C的张角为120°(∠A=120°),计算求出岛B和岛C的长度?【预设的答案】0【设计意图】从知识到应用,在回顾前面问题的基础上,加强对余弦定理的理解练习:在▲ABC中b=3,c=,A=30°,求a【预设的答案】【设计意图】在形成概念后,遵循从一般到特殊的思路,在实践活动中进行再认识,熟悉概念,从外延的角度加深概念的理解,为下一个环节作铺垫;同时也规范对数符号的书写.1.4升入理解,理性分析余弦定理:三角形任何一边的平方,等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍.即:abcbaC2cos222bca...