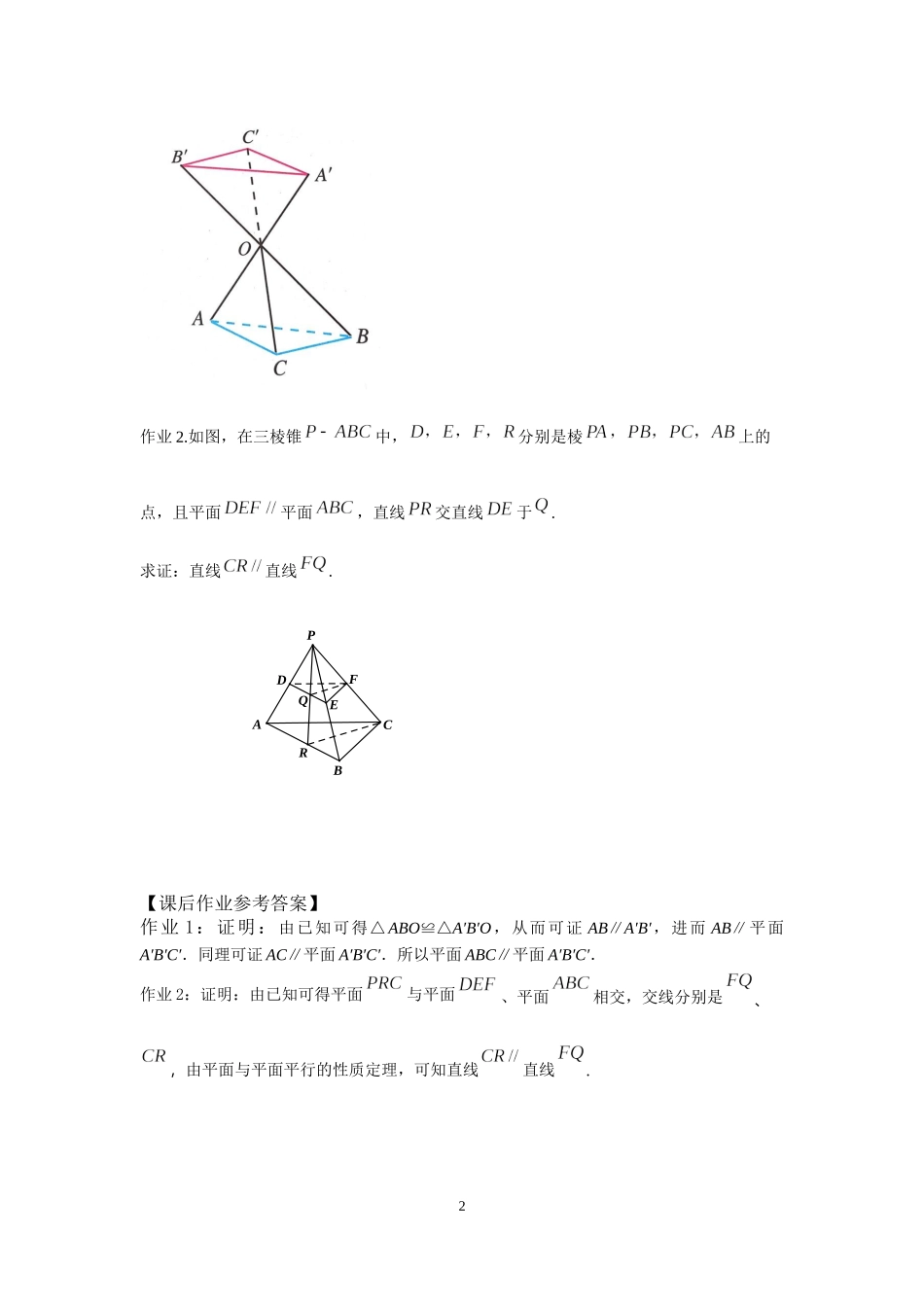
1《平面与平面平行》学习任务单【学习目标】结合具体实物探究并理解平面与平面平行的判定定理,培养学生观察问题和分析问题的能力,发展直观想象素养;探究并证明平面与平面平行的性质定理.,提升学生逻辑推理素养.【课上任务】1.能否将“一个平面内的任意直线平行另一个平面”中的“任意直线”减少,得到更简便的方法?2.“一个平面内两条平行直线与另一个平面平行”和“一个平面内两条相交直线与另一个平面平行”,能否判断这两个平面平行?3.为什么不能用一个平面内两条平行直线平行于另一个平面判断两个平面平行,而可以用两条相交直线平行另一个平面判断两个平面平行?联想平面向量基本定理,你能对面面平行判定定理做出进一步解释吗?4.平面与平面平行的判定定理是什么?5.平面与平面平行的判定定理有什么作用?6.在实际生活中,你见过工人师傅怎样判断两个平面平行吗?你能说明这么做的道理吗?7.类比直线与平面平行的研究,已知两个平面平行,我们可以得到哪些结论?8.平面与平面平行的性质定理是什么?9.平面与平面平行的性质定理有什么作用?【学习疑问】10.哪段文字没看明白?11.没看明白的文字,用自己的话怎么说?12.哪个环节没弄清楚?13.你想向同伴提出什么问题?14.你想向老师提出什么问题?15.本节课有几个环节,环节之间的联系和顺序是什么?【课后作业】作业1.如图,直线相交于点,,,.求证:平面平面.2作业2.如图,在三棱锥中,分别是棱上的点,且平面平面,直线交直线于.求证:直线直线.【课后作业参考答案】作业1:证明:由已知可得△ABO≌△A′B′O,从而可证AB∥A′B′,进而AB∥平面A′B′C′.同理可证AC∥平面A′B′C′.所以平面ABC∥平面A′B′C′.作业2:证明:由已知可得平面与平面、平面相交,交线分别是、,由平面与平面平行的性质定理,可知直线直线.FEDACBPQR