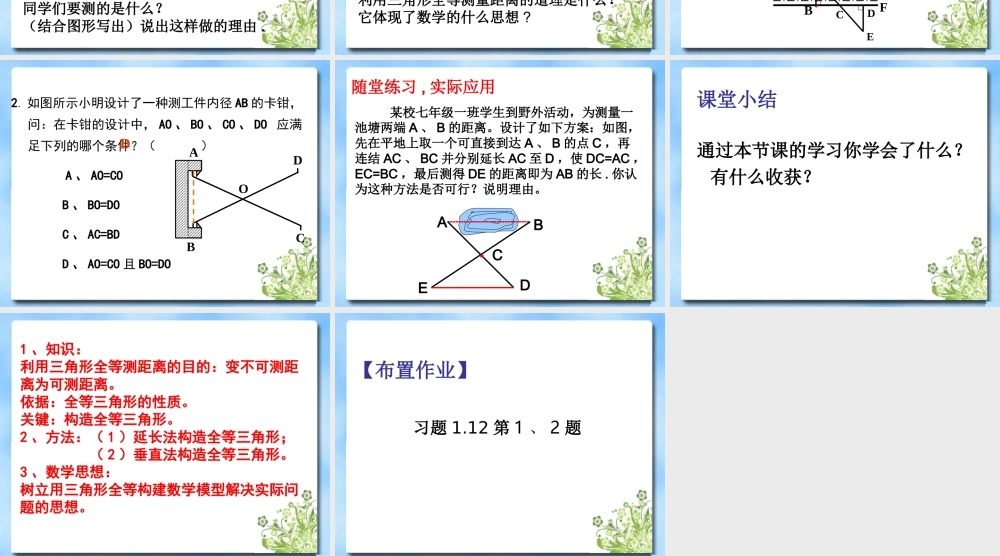
七年级数学(上)(第一章)1.5利用三角形全等测距离思考:你知道怎样测量河的宽度吗?【创设情境,导入新课】【教学目标】1.通过利用三角形全等解决实际问题,感受所学数学知识与实际生活的联系;2.能在解决问题的过程中进行有条理的思考与表达.(4)“SAS”:两边及其夹角分别相等的两个三角形全等.思考:要判定两个三角形全等有哪些方法?(1)“SSS”:三边分别相等的两个三角形全等.(3)“AAS”:两角分别相等且其中一组等角的对边相等的两个三角形全等.(2)“ASA”:两角及其夹边分别相等的两个三角形全等.全等三角形的性质是什么?【课中实施】自主学习,预习诊断合作探究,展示交流阅读课本第33页内容并回答下列问题.(1)画出相应的图形,并与同学进行交流.老师所讲述的方法中,已知条件是什么?同学们要测的是什么?(结合图形写出)说出这样做的理由.想一想如何测量池塘A、B两点间距离?小明和小颖讲述的方法中,已知条件是什么?要测的是什么?(结合图形写出理由)想一想:利用三角形全等测量距离的道理是什么?它体现了数学的什么思想?1.如图要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是()A、SSSB、ASAC、AASD、SASBA●●DCEFB2.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO应满足下列的哪个条件?()A、AO=COB、BO=DOC、AC=BDD、AO=CO且BO=DODODCBA某校七年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长AC至D,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?说明理由。C·ADEB随堂练习,实际应用课堂小结通过本节课的学习你学会了什么?有什么收获?1、知识:利用三角形全等测距离的目的:变不可测距离为可测距离。依据:全等三角形的性质。关键:构造全等三角形。2、方法:(1)延长法构造全等三角形;(2)垂直法构造全等三角形。3、数学思想:树立用三角形全等构建数学模型解决实际问题的思想。习题1.12第1、2题【布置作业】