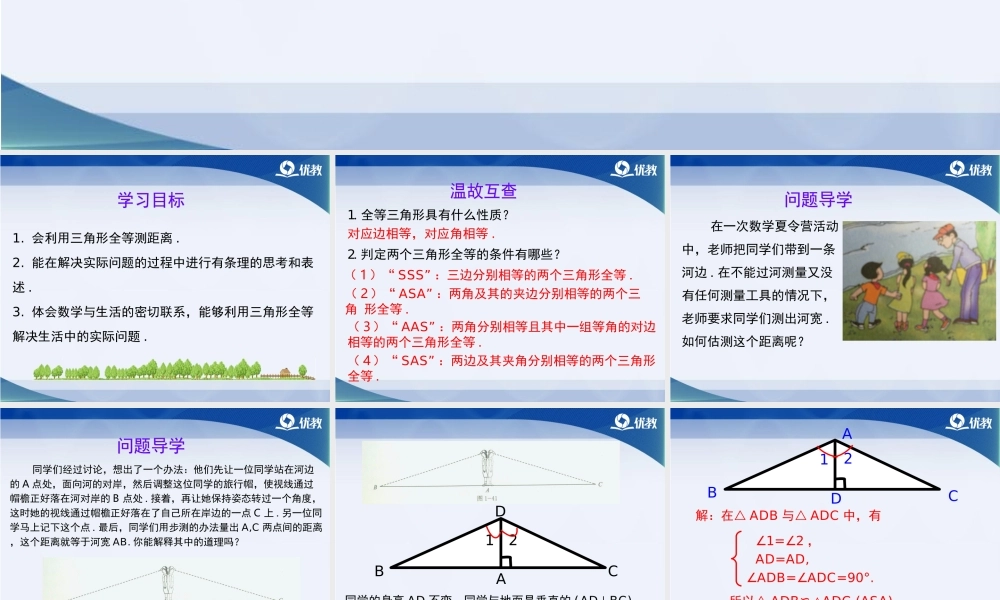
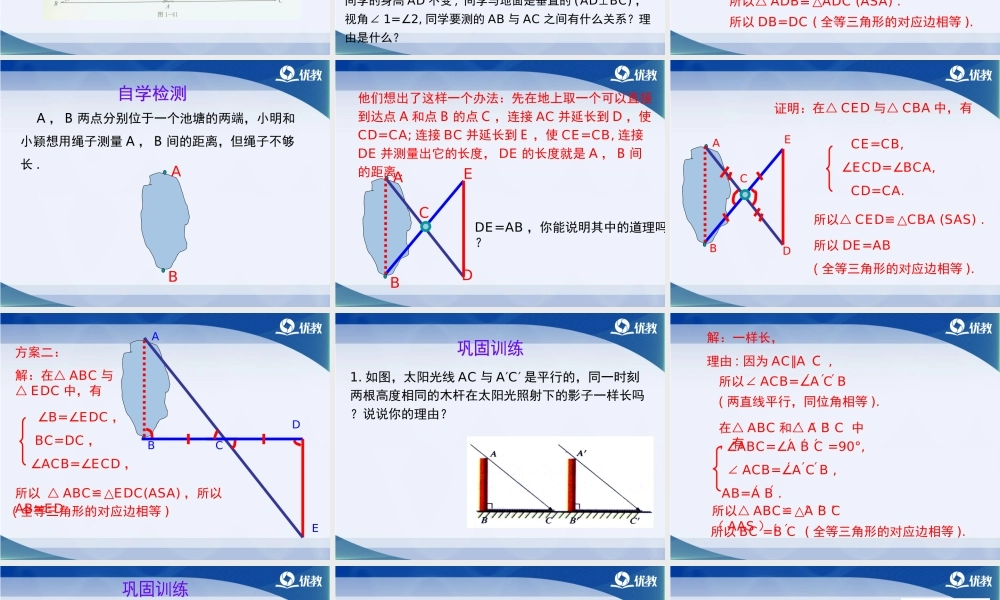
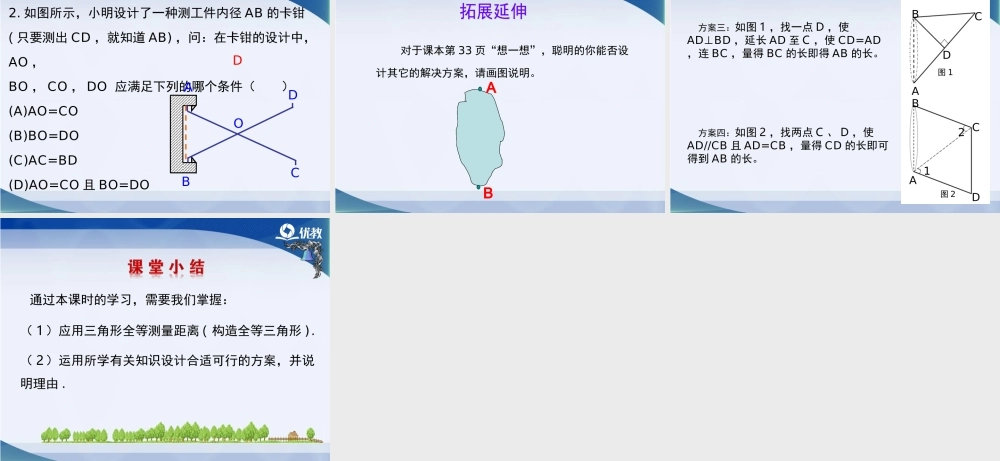
1.会利用三角形全等测距离.2.能在解决实际问题的过程中进行有条理的思考和表述.3.体会数学与生活的密切联系,能够利用三角形全等解决生活中的实际问题.1.全等三角形具有什么性质?对应边相等,对应角相等.2.判定两个三角形全等的条件有哪些?(1)“SSS”:三边分别相等的两个三角形全等.(2)“ASA”:两角及其的夹边分别相等的两个三角形全等.(3)“AAS”:两角分别相等且其中一组等角的对边相等的两个三角形全等.(4)“SAS”:两边及其夹角分别相等的两个三角形全等.在一次数学夏令营活动中,老师把同学们带到一条河边.在不能过河测量又没有任何测量工具的情况下,老师要求同学们测出河宽.如何估测这个距离呢?同学们经过讨论,想出了一个办法:他们先让一位同学站在河边的A点处,面向河的对岸,然后调整这位同学的旅行帽,使视线通过帽檐正好落在河对岸的B点处.接着,再让她保持姿态转过一个角度,这时她的视线通过帽檐正好落在了自己所在岸边的一点C上.另一位同学马上记下这个点.最后,同学们用步测的办法量出A,C两点间的距离,这个距离就等于河宽AB.你能解释其中的道理吗?同学的身高AD不变,同学与地面是垂直的(AD⊥BC),视角∠1=∠2,同学要测的AB与AC之间有什么关系?理由是什么?12DBAC12ABDC解:在△ADB与△ADC中,有∠1=∠2,AD=AD,∠ADB=∠ADC=90°.所以△ADB≌△ADC(ASA).所以DB=DC(全等三角形的对应边相等).A,B两点分别位于一个池塘的两端,小明和小颖想用绳子测量A,B间的距离,但绳子不够长.AB他们想出了这样一个办法:先在地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.ABCDEDE=AB,你能说明其中的道理吗?在△CED与△CBA中,有CE=CB,∠ECD=∠BCA,CD=CA.所以△CED≌△CBA(SAS).所以DE=AB(全等三角形的对应边相等).ABCDE证明:ABCDE∠B=∠EDC,BC=DC,∠ACB=∠ECD,所以△ABC≌△EDC(ASA),所以AB=ED解:在△ABC与△EDC中,有(全等三角形的对应边相等)方案二:1.如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由?解:一样长,理由:因为AC∥AC,所以∠ACB=∠ACB(两直线平行,同位角相等).′′′所以BC=BC(全等三角形的对应边相等).′′所以△ABC≌△ABC(AAS).′′′∠ABC=∠ABC=90°,∠ACB=∠ACB,AB=AB.′′′′′′′′在△ABC和△ABC中,有′′′2.如图所示,小明设...