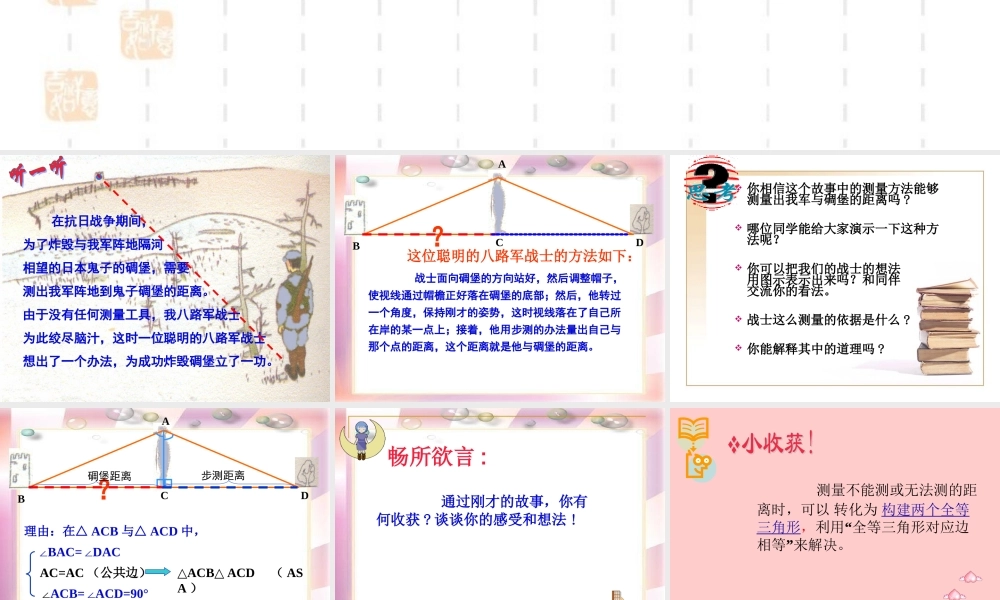
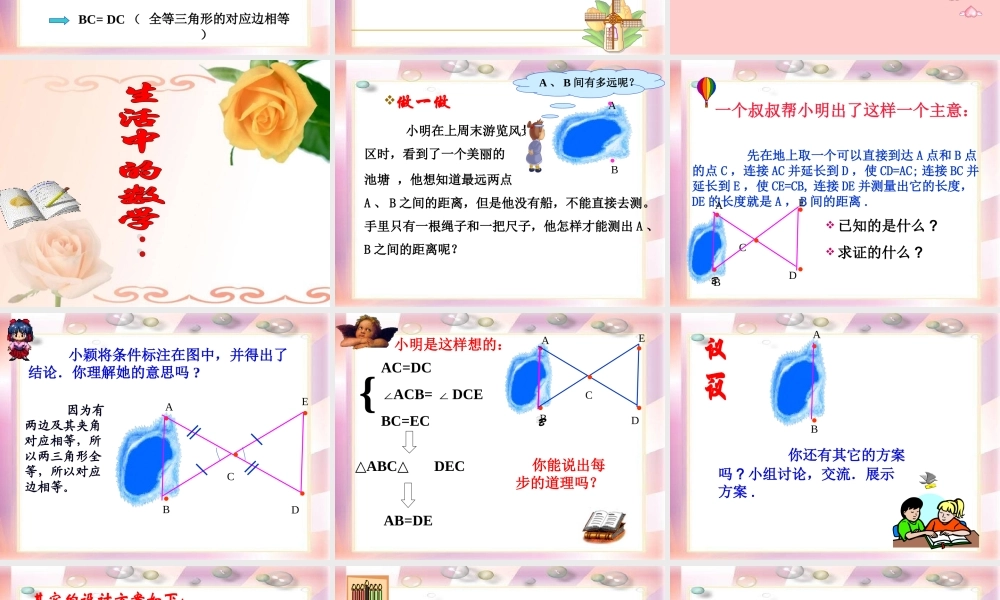
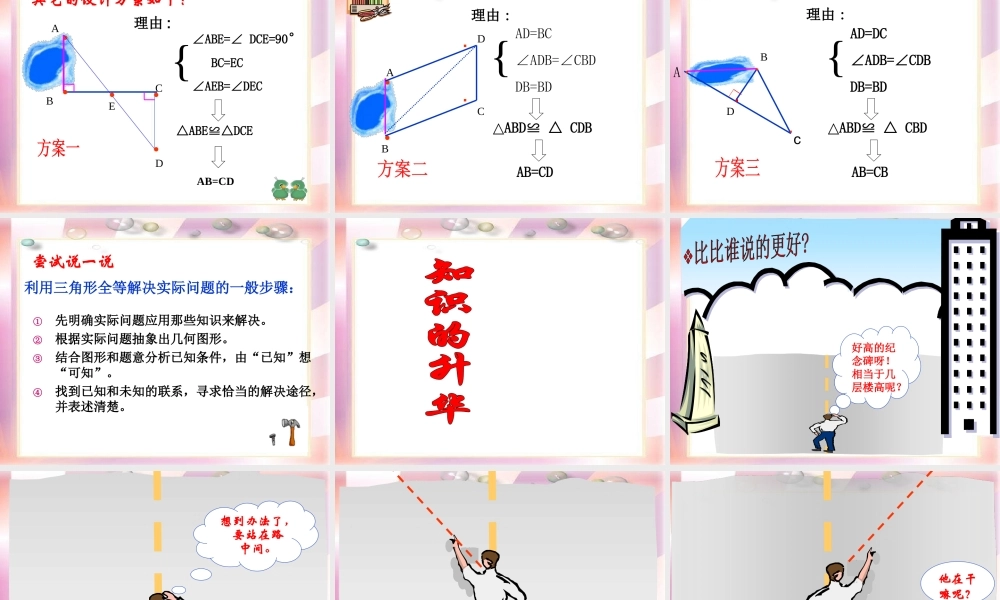
第一章三角形1.5利用三角形全等测距离在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。这位聪明的八路军战士的方法如下:战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。ACBD?你相信这个故事中的测量方法能够测量出我军与碉堡的距离吗?哪位同学能给大家演示一下这种方法呢?你可以把我们的战士的想法用图示表示出来吗?和同伴交流你的看法。战士这么测量的依据是什么?你能解释其中的道理吗?ACBD?BC=DC()理由:在△ACB与△ACD中,∠BAC=DAC∠AC=AC(公共边)∠ACB=ACD=90°∠△ACBACD△(ASA)全等三角形的对应边相等步测距离碉堡距离通过刚才的故事,你有何收获?谈谈你的感受和想法!畅所欲言:测量不能测或无法测的距离时,可以转化为构建两个全等三角形,“利用全等三角形对应边”相等来解决。::小明在上周末游览风景区时,看到了一个美丽的池塘,他想知道最远两点A、B之间的距离,但是他没有船,不能直接去测。手里只有一根绳子和一把尺子,他怎样才能测出A、B之间的距离呢?A、B间有多远呢?AB··做一做一个叔叔帮小明出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.已知的是什么?求证的什么?CBA·····DEBB小颖将条件标注在图中,并得出了结论.你理解她的意思吗?CBA·····DE因为有两边及其夹角对应相等,所以两三角形全等,所以对应边相等。小明是这样想的:CBA·····DEBB△ABC△DEC△AC=DC∠ACB=DCE∠BC=EC{AB=DE你能说出每步的道理吗?BA··你还有其它的方案吗?小组讨论,交流.展示方案.其它的设计方案如下:DCBA·E····△ABE≌△DCE∠ABE=∠DCE=90°BC=EC∠AEB=∠DEC{AB=CD理由:{△ABD≌△CDBAD=BC∠ADB=∠CBDDB=BDAB=CD理由:BA··CD···D{△ABD≌△CBDAD=DC∠ADB=∠CDBDB=BDAB=CBB理由:A.··c利用三角形全等解决实际问题的一般步骤:①先明确实际问题应用那些知识来解决。②根据实际问题抽象出几何图形。③结合图形...