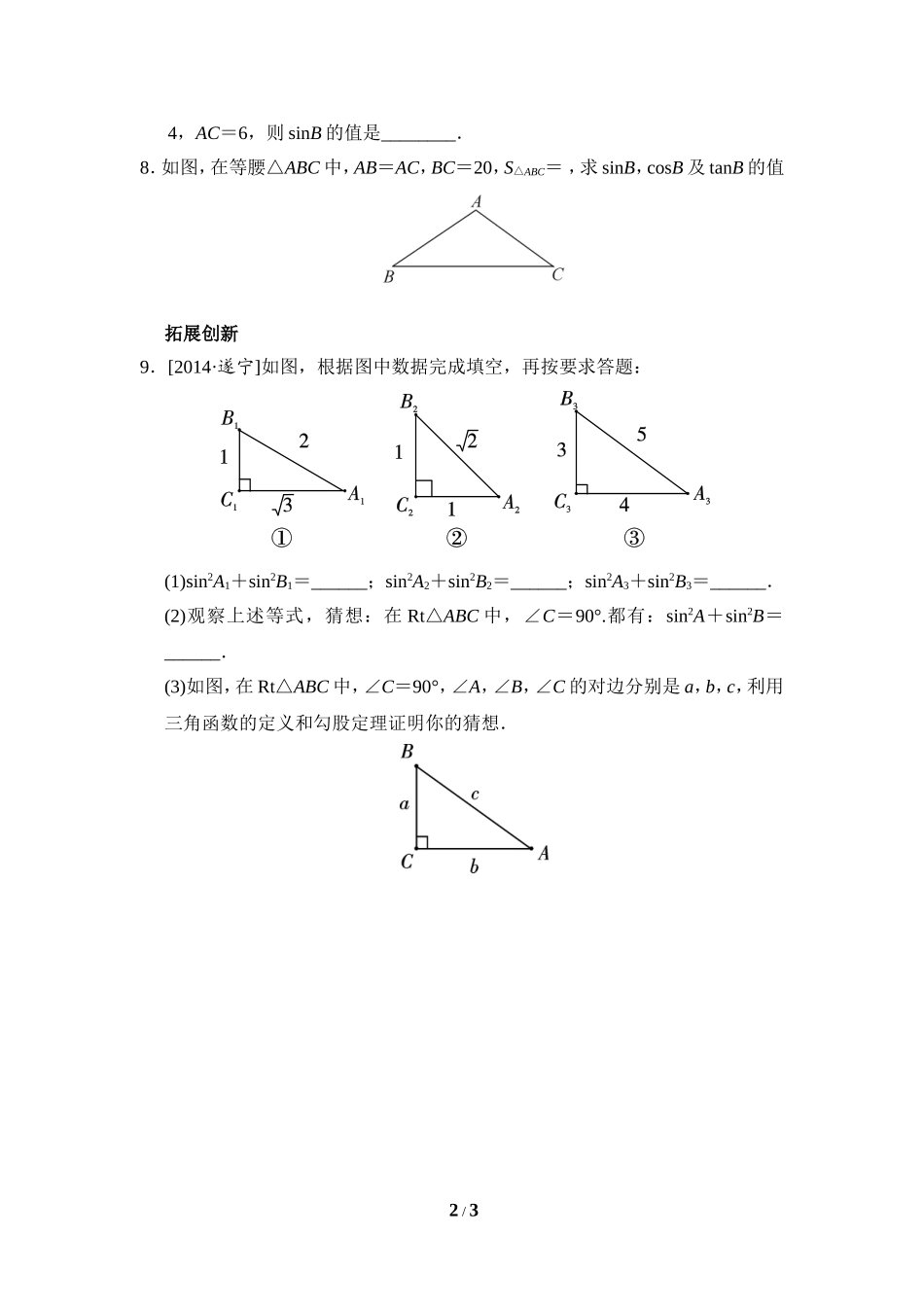
锐角三角函数(第2课时)基础达标1.[2013·兰州]△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是()A.csinA=aB.bcosB=cC.atanA=bD.ctanB=b2.[2013·连云港]在Rt△ABC中,∠C=90°,若sinA=,则cosA的值是()A.B.C.D.3.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB=()A.B.C.D.4.[2013·杭州]在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于()A.B.C.D.5.[2014·天水]如图,方格纸中的每个小正方形都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.若△ABC的顶点都在方格的格点上,则cosA=__________.6.在△ABC,∠C=90°,BC=2,AB=5,求sinA,cosA,tanA.能力提升7.[2014·齐齐哈尔]在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=1/34,AC=6,则sinB的值是________.8.如图,在等腰△ABC中,AB=AC,BC=20,S△ABC=,求sinB,cosB及tanB的值拓展创新9.[2014·遂宁]如图,根据图中数据完成填空,再按要求答题:(1)sin2A1+sin2B1=______;sin2A2+sin2B2=______;sin2A3+sin2B3=______.(2)观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=______.(3)如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理证明你的猜想.2/3参考答案1.A2.D3.C4.B5.6.sinA=,cosA=,tanA=7.8.sinB=,cosB=,tanB=9.(1)111(2)1(3)略3/3