1.1.2 锐角三角函数（2）.pptxVIP免费

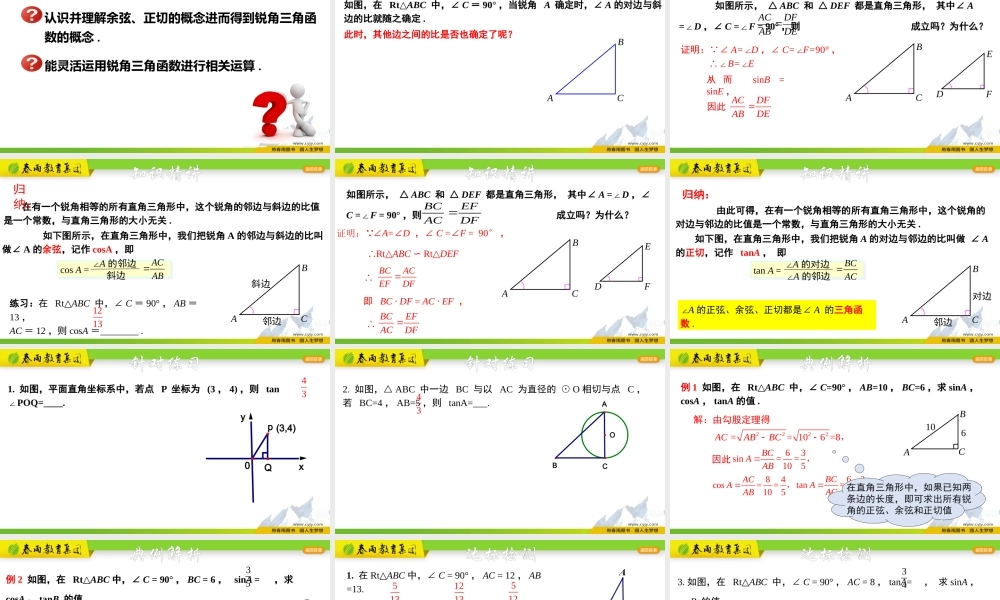
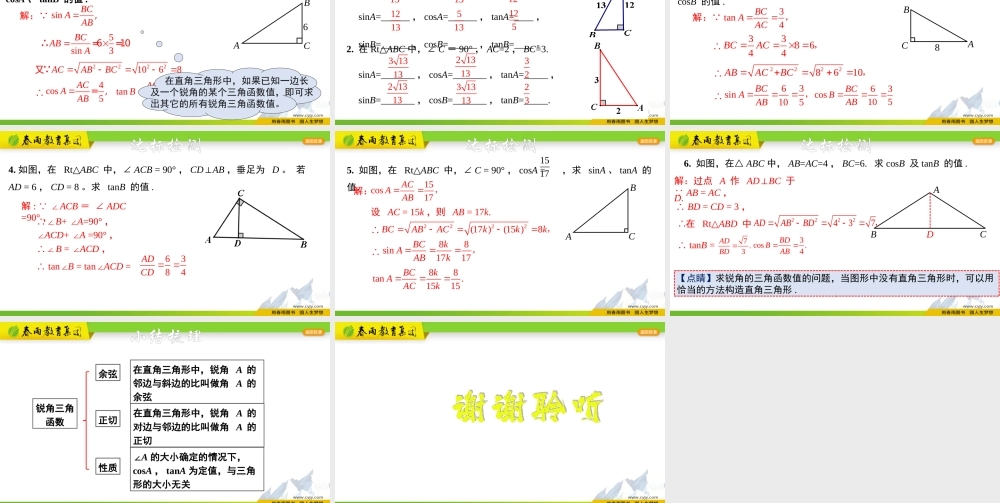
浙教版·九年级下册学习目标认识并理解余弦、正切的概念进而得到锐角三角函数的概念.能灵活运用锐角三角函数进行相关运算.ABC如图，在Rt△ABC中，∠C＝90°，当锐角A确定时，∠A的对边与斜边的比就随之确定.此时，其他边之间的比是否也确定了呢？问题引入知识精讲如图所示，△ABC和△DEF都是直角三角形，其中∠A=∠D，∠C=∠F=90°，则成立吗？为什么？DEDFABACABCDEF证明： ∠A=∠D，∠C=∠F=90°，∴∠B=∠E，从而sinB=sinE，因此ACDFABDE在有一个锐角相等的所有直角三角形中，这个锐角的邻边与斜边的比值是一个常数，与直角三角形的大小无关.如下图所示，在直角三角形中，我们把锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即归纳：ABC斜边邻边∠A的邻边斜边cosA=ACAB知识精讲练习：在Rt△ABC中，∠C＝90°，AB＝13，AC＝12，则cosA＝.1213如图所示，△ABC和△DEF都是直角三角形，其中∠A=∠D，∠C=∠F=90°，则成立吗？为什么？DFEFACBCABCDEF∴Rt△ABCRt∽△DEF即BC·DF=AC·EF，∠A=∠D，∠C=∠F=90°，证明： ∴BCACEFDF∴BCEFACDF知识精讲由此可得，在有一个锐角相等的所有直角三角形中，这个锐角的对边与邻边的比值是一个常数，与直角三角形的大小无关.如下图，在直角三角形中，我们把锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即归纳：∠A的对边∠A的邻边tanA=BCACABC邻边对边∠A的正弦、余弦、正切都是∠A的三角函数.知识精讲Q(3,4)0pyx1.如图，平面直角坐标系中，若点P坐标为(3，4)，则tanPOQ=____.∠43针对练习OCBA2.如图，△ABC中一边BC与以AC为直径的⊙O相切与点C，若BC=4，AB=5，则tanA=___.43针对练习例1如图，在Rt△ABC中，∠C=90°，AB=10，BC=6，求sinA，cosA，tanA的值.ABC106解：由勾股定理得2222==106=8ACABBC，因此63sin==105BCAAB，84cos==105ACAAB，63tan==84BCAAC在直角三角形中，如果已知两条边的长度，即可求出所有锐角的正弦、余弦和正切值典例解析ABC6例2如图，在Rt△ABC中，∠C=90°，BC=6，sinA=，求cosA、tanB的值.35解： sinBCAAB，5sin3BCABA∴=6=10又22221068ACABBC 4tan3ACBBC=4cos5ACAAB=，∴在直角三角形中，如果已知一边长及一个锐角的某个三角函数值，即可求出其它的所有锐角三角函数值。典例解析1.在Rt△ABC中，∠C=90°，AC=12，AB=13.sinA=______，cosA=______，tanA=____，sinB=______，cosB=______，tanB=____。513121351251312131252....