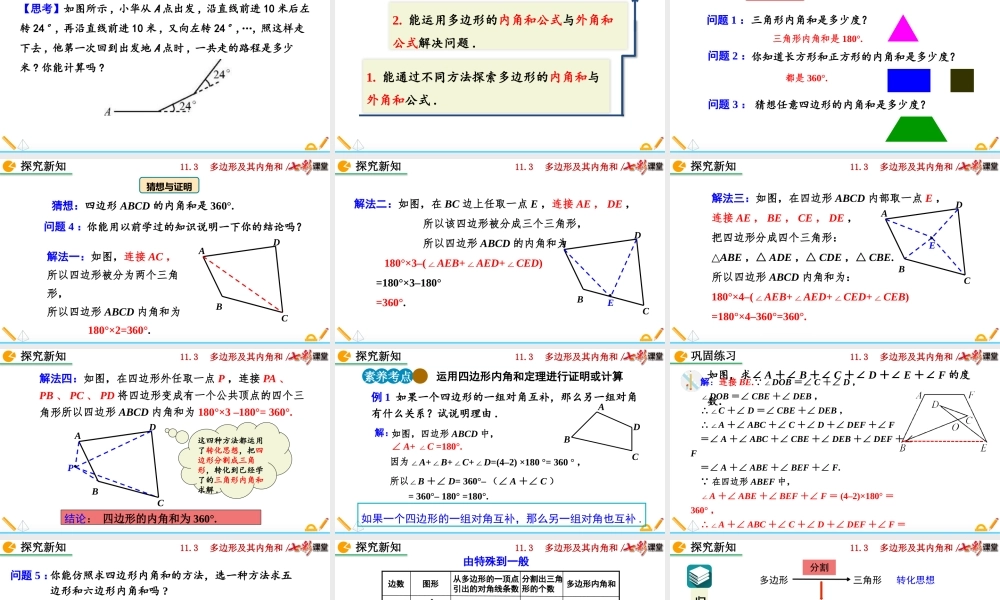
11.3多边形及其内角和/11.3多边形及其内角和11.3.2多边形的内角和人教版数学八年级上册11.3多边形及其内角和/【思考】如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是多少米?你能计算吗?导入新知11.3多边形及其内角和/1.能通过不同方法探索多边形的内角和与外角和公式.2.能运用多边形的内角和公式与外角和公式解决问题.素养目标11.3多边形及其内角和/你知道长方形和正方形的内角和是多少度?三角形内角和是多少度?三角形内角和是180°.都是360°.猜想任意四边形的内角和是多少度?多边形的内角和探究新知知识点1问题1:问题2:问题3:11.3多边形及其内角和/猜想:四边形ABCD的内角和是360°.你能用以前学过的知识说明一下你的结论吗?解法一:如图,连接AC,所以四边形被分为两个三角形,所以四边形ABCD内角和为180°×2=360°.ABCD探究新知猜想与证明问题4:11.3多边形及其内角和/解法二:如图,在BC边上任取一点E,连接AE,DE,所以该四边形被分成三个三角形,所以四边形ABCD的内角和为180°×3–(∠AEB+∠AED+∠CED)=180°×3–180°=360°.ABCDE探究新知11.3多边形及其内角和/解法三:如图,在四边形ABCD内部取一点E,连接AE,BE,CE,DE,把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.所以四边形ABCD内角和为:180°×4–(∠AEB+∠AED+∠CED+∠CEB)=180°×4–360°=360°.ABCDE探究新知11.3多边形及其内角和/ABCDP解法四:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.所以四边形ABCD内角和为180°×3–180°=360°.这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.结论:四边形的内角和为360°.探究新知11.3多边形及其内角和/例1如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.解:如图,四边形ABCD中,∠A+∠C=180°.∠A+∠B+∠C+∠D=(4–2)×180°=360°,因为∠B+∠D=360°–(∠A+∠C)=360°–180°=180°.所以ABCD如果一个四边形的一组对角互补,那么另一组对角也互补.素养考点1运用四边形内角和定理进行证明或计算探究新知11.3多边形及其内角和/如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.巩固练习解:连接BE. ∠DOB=∠C+∠D,∠DOB=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,∴∠A+∠ABC+∠C+∠D+∠DE...