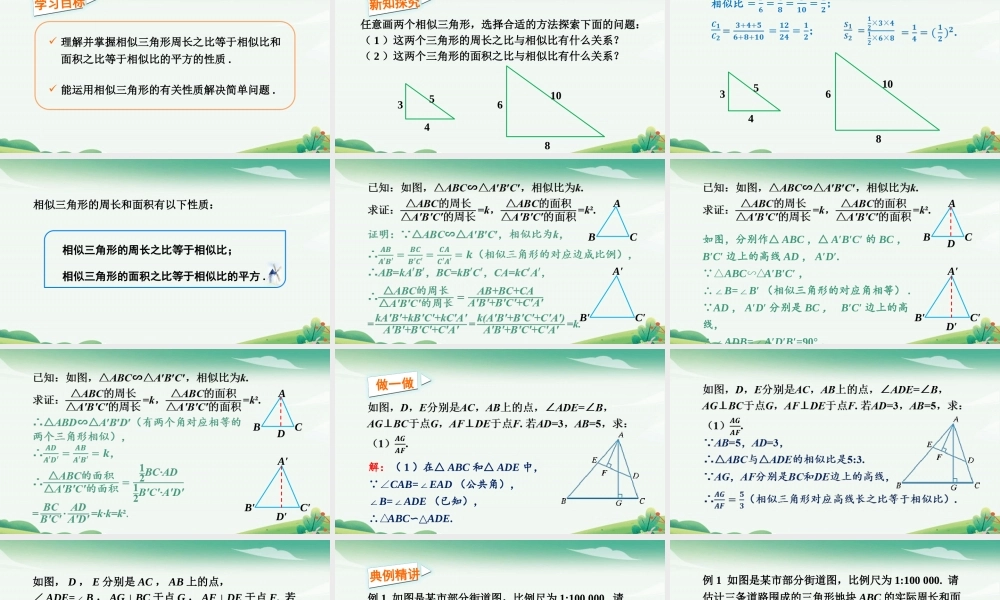
4.5相似三角形的性质及其应用第2课时相似三角形的性质(2)学习目标理解并掌握相似三角形周长之比等于相似比和面积之比等于相似比的平方的性质.能运用相似三角形的有关性质解决简单问题.新知探究任意画两个相似三角形,选择合适的方法探索下面的问题:(1)这两个三角形的周长之比与相似比有什么关系?(2)这两个三角形的面积之比与相似比有什么关系?34568103456810相似比相似三角形的周长之比等于相似比;相似三角形的面积之比等于相似比的平方.相似三角形的周长和面积有以下性质:ABCA′B′C′ABCA′B′C′如图,分别作△ABC,△A′B′C′的BC,B′C′边上的高线AD,A′D′.∵△ABC∽△A′B′C′,∴∠B=∠B′(相似三角形的对应角相等).∵AD,A′D′分别是BC,B′C′边上的高线,∴∠ADB=∠A′D′B′=90°DD′ABCA′B′C′DD′做一做解:(1)在△ABC和△ADE中,∵∠CAB=∠EAD(公共角),∠B=∠ADE(已知),∴△ABC∽△ADE.如图,D,E分别是AC,AB上的点,∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F.若AD=3,AB=5,求:(2)△ADE与△ABC的周长之比.(3)△ADE与△ABC的面积之比.(2)△ADE与△ABC的周长之比是3:5(相似三角形的周长之比等于相似比).(3)△ADE与△ABC的面积之比是9:25(相似三角形的面积之比等于相似比的平方).典例精讲例1如图是某市部分街道图,比例尺为1:100000.请估计三条道路围成的三角形地块ABC的实际周长和面积.例1如图是某市部分街道图,比例尺为1:100000.请估计三条道路围成的三角形地块ABC的实际周长和面积.例1如图是某市部分街道图,比例尺为1:100000.请估计三条道路围成的三角形地块ABC的实际周长和面积.例2如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,则AD与AB的比应取多少?例2如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,则AD与AB的比应取多少?课堂小结三角形相似的性质(2)周长比面积比=相似比=相似比的平方当堂检测1.填空:(1)如果三角形的边长扩大到原来的100倍,那么三角形的周长扩大到原来的______倍;面积扩大到原来的______倍.(2)如果三角形的周长扩大到原来的100倍,那么三角形的边长扩大到原来的______倍.(3)如果三角形的面积扩大到原来的100倍,那么三角形的边长扩大到原来的______倍.10010100100002.如图,在等边三角形ABC中,点D,E分别在边AB,AC上,DE∥BC.如果BC=8cm,AD:DB=1:3,则△ADE的周长等于______cm,△ADE的面积等于______cm2.6感谢观看!