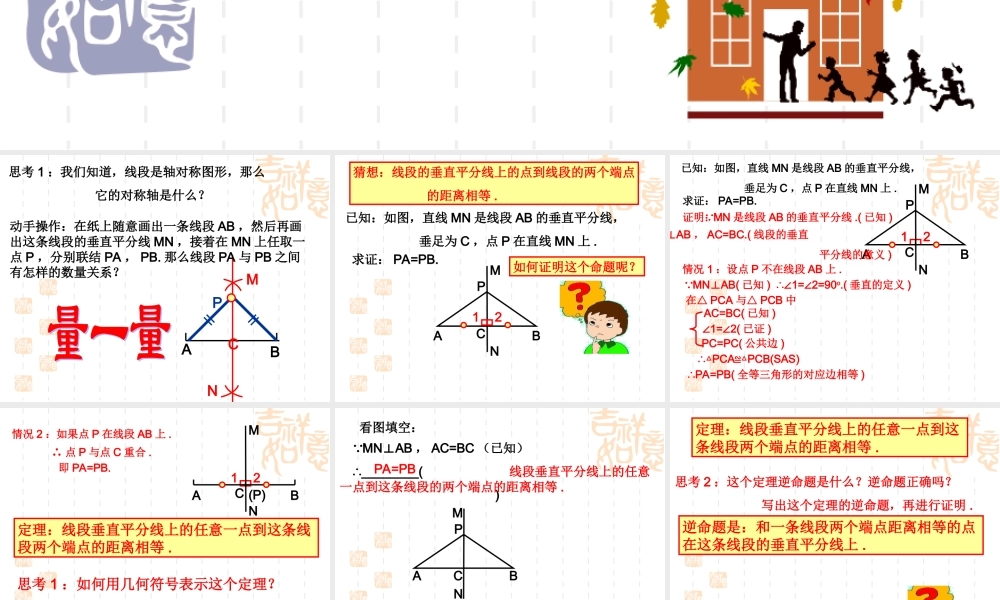
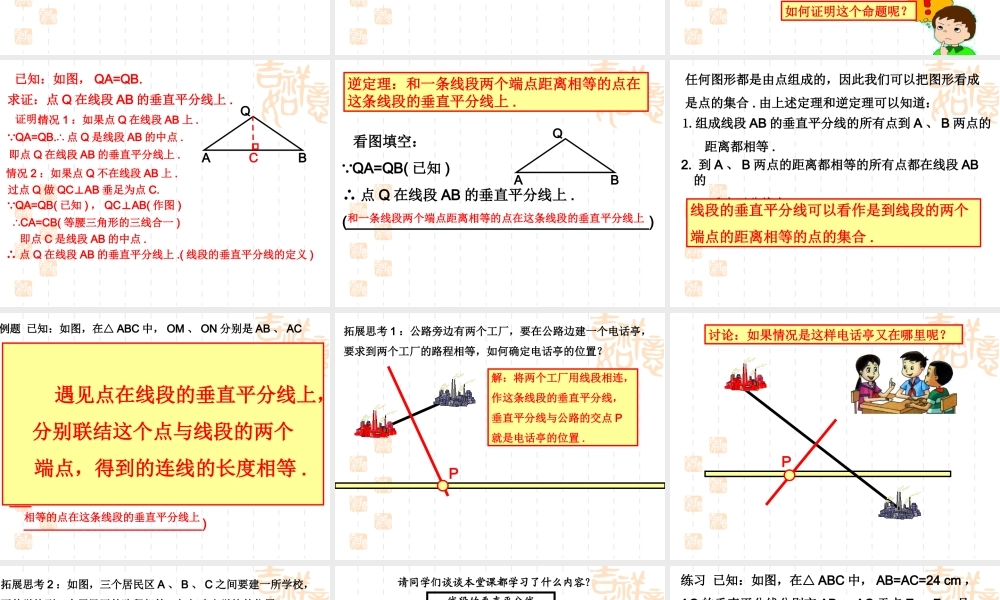
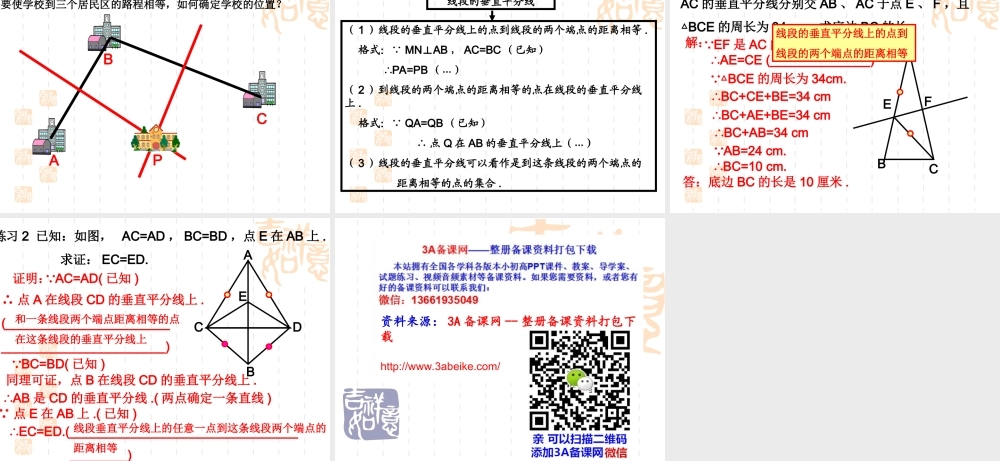
19.4线段的垂直平分线思考1:我们知道,线段是轴对称图形,那么它的对称轴是什么?ABMN动手操作:在纸上随意画出一条线段AB,然后再画出这条线段的垂直平分线MN,接着在MN上任取一点P,分别联结PA,PB.那么线段PA与PB之间有怎样的数量关系?PC猜想:线段的垂直平分线上的点到线段的两个端点的距离相等.已知:如图,直线MN是线段AB的垂直平分线,垂足为C,点P在直线MN上.AMPNBC求证:PA=PB.如何证明这个命题呢?12已知:如图,直线MN是线段AB的垂直平分线,垂足为C,点P在直线MN上.AMPNBC求证:PA=PB.证明:12 MN是线段AB的垂直平分线.(已知)AB⊥,AC=BC.(线段的垂直平分线的意义)情况1:设点P不在线段AB上. MNAB(⊥已知)1=2=90∴∠∠o.(垂直的定义)在△PCA与△PCB中AC=BC(已知)∠1=2(∠已证)PC=PC(公共边)∴△PCAPCB(SAS)≌△∴PA=PB(全等三角形的对应边相等)AM(P)NBC12情况2:如果点P在线段AB上.∴点P与点C重合.即PA=PB.定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.思考1:如何用几何符号表示这个定理?∴________()线段垂直平分线上的任意一点到这条线段的两个端点的距离相等.AMPNBC看图填空: MNAB⊥,AC=BC(已知)PA=PB定理:线段垂直平分线上的任意一点到这条线段两个端点的距离相等.思考2:这个定理逆命题是什么?逆命题正确吗?写出这个定理的逆命题,再进行证明.逆命题是:和一条线段两个端点距离相等的点在这条线段的垂直平分线上.如何证明这个命题呢?AQBC已知:如图,QA=QB.求证:点Q在线段AB的垂直平分线上.证明:情况1:如果点Q在线段AB上. QA=QB.∴点Q是线段AB的中点.即点Q在线段AB的垂直平分线上.情况2:如果点Q不在线段AB上.过点Q做QCAB⊥垂足为点C. QA=QB(已知),QCAB(⊥作图)∴CA=CB(等腰三角形的三线合一)即点C是线段AB的中点.∴点Q在线段AB的垂直平分线上.(线段的垂直平分线的定义)逆定理:和一条线段两个端点距离相等的点在这条线段的垂直平分线上.AQB看图填空: QA=QB(已知)∴点Q在线段AB的垂直平分线上.(_____________________________________)和一条线段两个端点距离相等的点在这条线段的垂直平分线上任何图形都是由点组成的,因此我们可以把图形看成是点的集合.由上述定理和逆定理可以知道:1.组成线段AB的垂直平分线的所有点到A、B两点的距离都相等.2.到A、B两点的距离都相等的所有点都在线段AB的垂直平分线上.线段的垂直平分线可以看作是到线段的两个端点的距离相等的点的集合.到线段的两个...