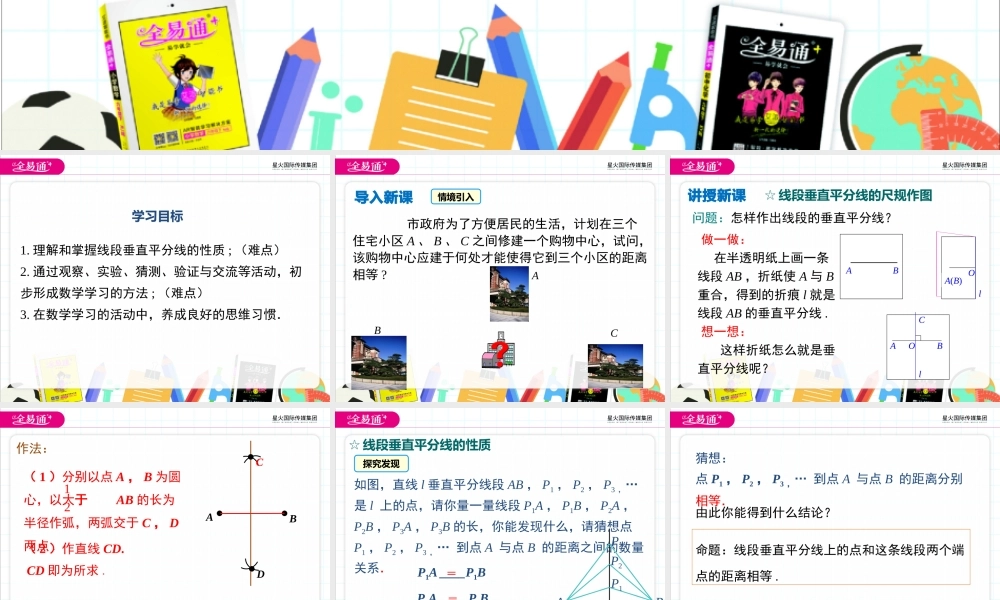
第15章轴对称图形与等腰三角形15.2线段的垂直平分线1.理解和掌握线段垂直平分线的性质;(难点)2.通过观察、实验、猜测、验证与交流等活动,初步形成数学学习的方法;(难点)3.在数学学习的活动中,养成良好的思维习惯.学习目标导入新课情境引入市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处才能使得它到三个小区的距离相等?ABC讲授新课☆线段垂直平分线的尺规作图问题:怎样作出线段的垂直平分线?做一做:在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.想一想:这样折纸怎么就是垂直平分线呢?ABA(B)ABlOlCOABCD作法:(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点.12(2)作直线CD.CD即为所求.特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.☆线段垂直平分线的性质如图,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么,请猜想点P1,P2,P3,…到点A与点B的距离之间的数量关系.ABlP1P2P3探究发现P1A____P1BP2A____P2BP3A____P3B===猜想:点P1,P2,P3,…到点A与点B的距离分别相等.命题:线段垂直平分线上的点和这条线段两个端点的距离相等.由此你能得到什么结论?你能验证这一结论吗?已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上.求证:PA=PB.证明: l⊥AB,∴∠PCA=∠PCB.又AC=CB,PC=PC,∴△PCA≌△PCB(SAS).∴PA=PB.PABlC验证结论例1如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为()A.5cmB.10cmC.15cmD.17.5cm典例精析C解析: △DBC的周长为BC+BD+CD=35cm,又 DE垂直平分AB,∴AD=BD,故BC+AD+CD=35cm.AC =AD+DC=20cm,∴BC=35-20=15(cm).故选C.方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.练一练:1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为()A.6B.5C.4D.32.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长是.B10cmPABCD图①ABCDE图②例2如图,已知点A、点B以及直线l.(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);(2)在...