沪教版数学八上17.4《一元二次方程的应用》课件2.pptVIP免费

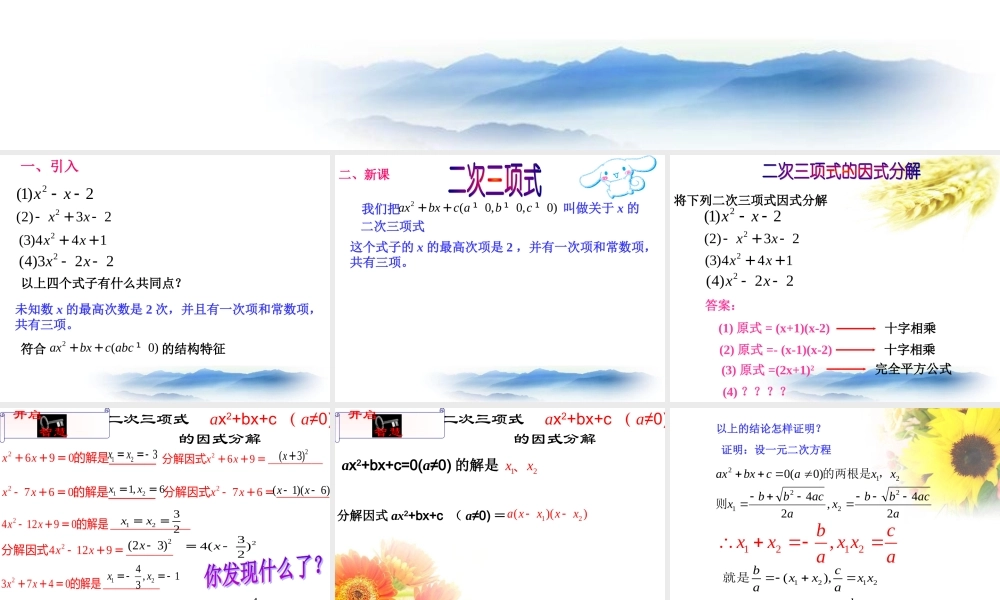
一、引入2)1(2xx2(2)32xx-+-以上四个式子有什么共同点？符合的结构特征2(0)axbxcabc++¹未知数x的最高次数是2次，并且有一次项和常数项，共有三项。2(4)322xx--2(3)441xx++二、新课这个式子的x的最高次项是2，并有一次项和常数项，共有三项。我们把2(0,0,0)axbxcabc++¹¹¹叫做关于x的二次三项式答案：(1)原式=(x+1)(x-2)(2)原式=-(x-1)(x-2)(4)？？？？2)1(2xx2(2)32xx-+-2(4)22xx--将下列二次三项式因式分解2(3)441xx++(3)原式=(2x+1)2十字相乘十字相乘完全平方公式二次三项式ax2+bx+c（a≠0)的因式分解269__________xx++=分解因式2690xx++=的解是________开启智慧2760xx-+=的解是________276_________xx-+=分解因式241290_______________xx-+=的解是24129________xx-+=分解因式23740___________xx++=的解是2374_______________xx++=分解因式123xx==-2(3)x+121,6xx==(1)(6)xx--1232xx==2(23)x-234()2x=-124,13xx=-=-(34)(1)xx++43()(1)3xx=++二次三项式ax2+bx+c（a≠0)的因式分解ax2+bx+c=0(a≠0)的解是分解因式ax2+bx+c（a≠0)＝12xx、12()()axxxx--开启智慧以上的结论怎样证明？证明：设一元二次方程aacbbxaacbbxxxacbxax24,24)0(02221212则，的两根是121222(),()bcxxxxaabcaxbxcaxxaa就是))((])([2121212xxxxaxxxxxxa1212,bcxxxxaa一般地,要在实数范围内分解二次三项式ax2+bx+c(a≠0),只要用公式法求出相应的一元二次方程ax2+bx+c=0(a≠0),的两个根x1,x2,然后直接将ax2+bx+c写成a(x-x1)(x-x2),就可以了.即ax2+bx+c=a(x-x1)(x-x2).:把下列各式分解因式开启智慧二次三项式ax2+bx+c的因式分解(13)(13)xx=-+--∴222xx--222xx--解：对于方程，2220xx--=2412bac-=1213,13xx=-=+这两方程的实数根是用合适的方法将下列二次三项式因式分解2(1)23xx--2(2)69xx-+3)(1)xx-+解：原式=(23)x-解：原式=(2(3)25xx--2216xx=-+-解：原式2(1)6x=--(16)(16)xx=-+--十字相乘完全平方公式配方法用合适的方法将下列二次三项式因式分解2(4)35xx--212329329350,22xxxx+---===解：方程的根是232932935()()22xxxx+-\--=--求根公式法用求根公式分解二次三项式)0(2acbxax其程序是固定的，即：（1）第一步：令02cbxax（2）第二步：求出方程①的两个根;,21xx①；（3）因式分解))((212xxxxacbxax二次三项式的因式分解常见方法通常有：十字相乘完全平方公式配方法求根公...