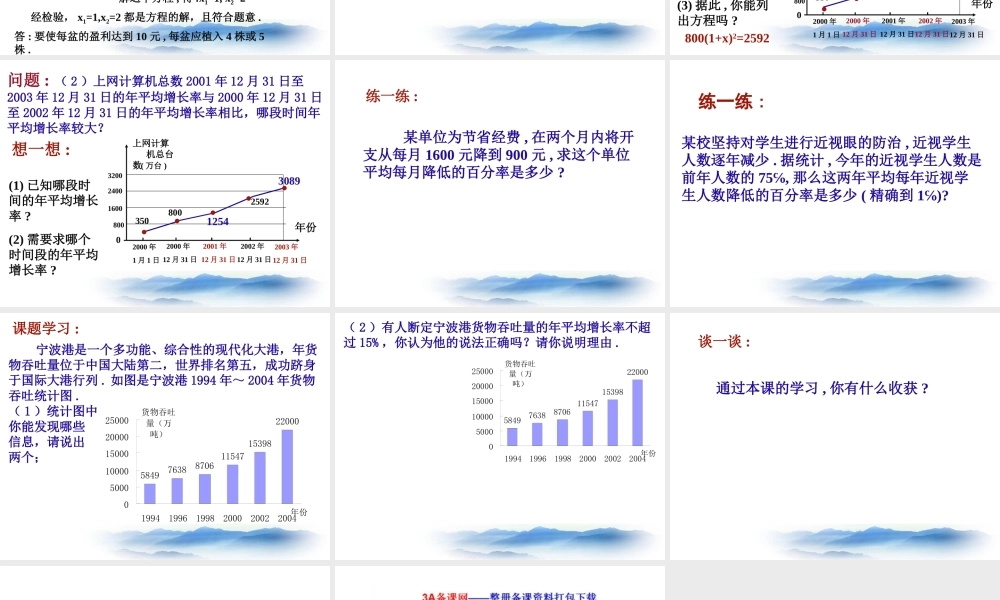
17.4一元二次方程的应用情境引入:小明想买一台电脑,他爸爸答应了,但有个条件:只要他解决了下面的问题,就给他买.问题是这样的:要做一个高是8cm,底面长比宽多5cm,体积528cm3的长方体木箱,问底面的长和宽是多少?如果你是小明,你能得到这台电脑吗?8cm长宽528cm3解:设长方体的宽为x(cm),则长为______cm,底面积为_______cm.长方体的底面积×高=长方体体积(528cm)列方程:化简、整理后,得解得x1=-11,x2=6检验:x1=-11<0不符合实际情况,舍去.当x2=6时,符合题意∴x=6∴长方体的长为6+5=11答:长方体的宽为6cm,长为11cm.找相等关系:(x+5)x(x+5)x(x+5)×8=528x2+5x-66=0回顾:列方程解应用题的基本步骤怎样?(1)审题:找出题中的量,分清有哪些已知量、未知量,哪些是要求的未知量和所涉及的基本数量关系、相等关系;(2)设:设元,包括设直接未知数或间接未知数;用所设的未知数字母的代数式表示其他的相关量;(3)列:列方程(一元二次方程);(4)解:解方程;(5)检验并作答:注意根的准确性及是否符合实际意义。问题1.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?如果直接设每盆植x株,怎样表示问题中相关的量?解:设每盆花苗增加的株数为x株,则每盆花苗有______株,平均单株盈利为__________元.相等关系:平均单株盈利×株数=10元由题意,得(x+3)(3-0.5x)=10解这个方程,得:x1=1,x2=2(x+3)(3-0.5x)如果设每盆花苗增加的株数为x株呢?思考:这个问题设什么为x?有几种设法?化简,整理,得x2-3x+2=0经检验,x1=1,x2=2都是方程的解,且符合题意.答:要使每盆的盈利达到10元,每盆应植入4株或5株.练一练:1.已知两个连续正奇数的积是63,利用一元二次方程求这两个数.问题2.截止到2000年12月31日,我国的上网计算机总数为800万台;截止到2002年12月31日,我国的上网计算机总数以达2592万台.(1)求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率(精确到0.1%).思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗?(2)已知2002年的台数是多少?(3)据此,你能列出方程吗?800(1+x)2=2592.....年份上网计算机总台数(万台)32002400160080002000年1月1日2000年12月31日2001年12月31日2002年12月31日2003年12月31日350800125425923089问题:(2)上网计算机总数2001年...