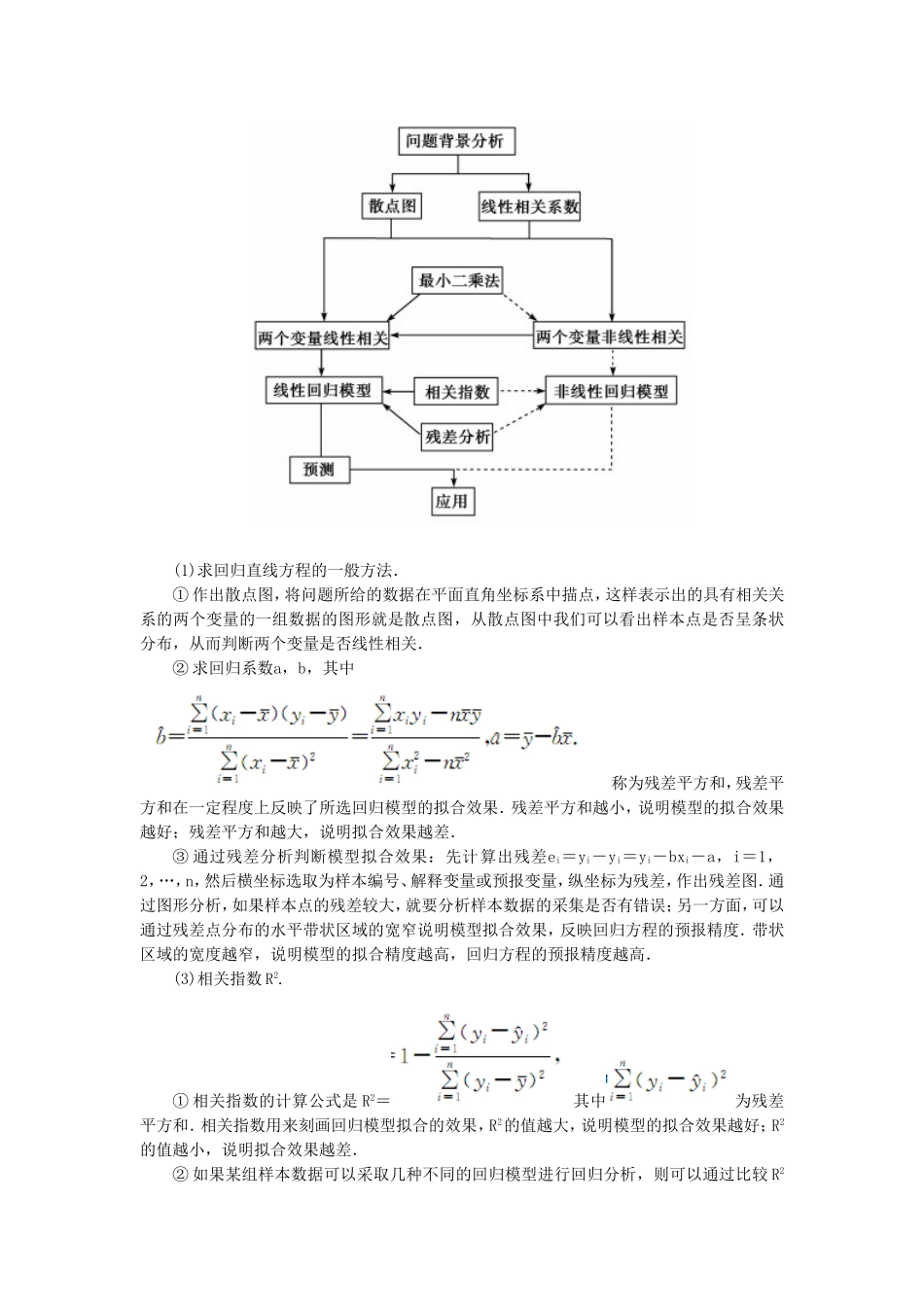
1.1回归分析的基本思想及其初步应用1.相关关系是一种非确定性关系,回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法,函数关系是一种确定性关系.2.在线性回归模型y=bx+a+e中,最小二乘法估计a和b就是未知参数a和b的最好估计,其计算公式如下:b=,a=,其中,x=i,y=i.另外,称为样本点的中心,回归直线一定过样本点中心.3.衡量模型拟合效果.(1)残差:对于样本点(x1,y1),(x2,y2),…,(xn,yn)而言,它们的随机误差为ei=yi-bxi-a,i=1,2,3,…,n,其估计值为ei=yi-yi=yi-bxi-a,i=1,2,…,n,ei称为相应于点(xi,yi)的残差.(2)残差图:我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号、身高数据或体重估计值等,这样作出的图形称为残差图.残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适.这样的带状区域的宽度越窄,说明模型拟合精度越高.(3)残差分析:可以通过残差发现原始数据中的可疑数据,判断所建立模型的拟合效果.(4)相关指数:计算公式是R2=.其中残差平方和为总偏差平方和为R2的值越大说明残差平方和越小,也就是说模型的拟合效果越好,R2的值表示解释变量对预报变量变化的贡献率,R2的值越接近于1,表示回归的效果越好.,1.下列结论正确的是(C)①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.A.①②B.①②③C.①②④D.①②③④解析:根据函数关系、相关关系、回归分析的概念可知选C.2.下列有关回归直线方程y=bx+a的叙述:①反映y与x之间的函数关系;②反映y与x之间的函数关系;③表示y与x之间不确定关系;④表示最接近y与x之间真实关系的一条直线.其中正确的是(D)A.①②B.②③C.③④D.①④解析:y=bx+a表示y与x之间的函数关系,而不是y与x之间的函数关系,但它反映的关系最接近y与x之间的真实关系.故选D.3.已知回归方程y=2x+1,而试验得到一组数据是(2,4.9),(3,7.1),(4,9.1),则残差平方和是(C)A.0.01B.0.02C.0.03D.0.04解析:(4.9-5)2+(7.1-7)2+(9.1-9)2=0.03.故选C.4.有下列数据:x123y35.9912.01下列四个函数中,模拟效果最好的为(A)A.y=3×2x-1B.y=log2xC.y=3xD.y=x2解析:当x=1,2,3时,分别代入求y值,离y最近的值模拟效果最好,知A...