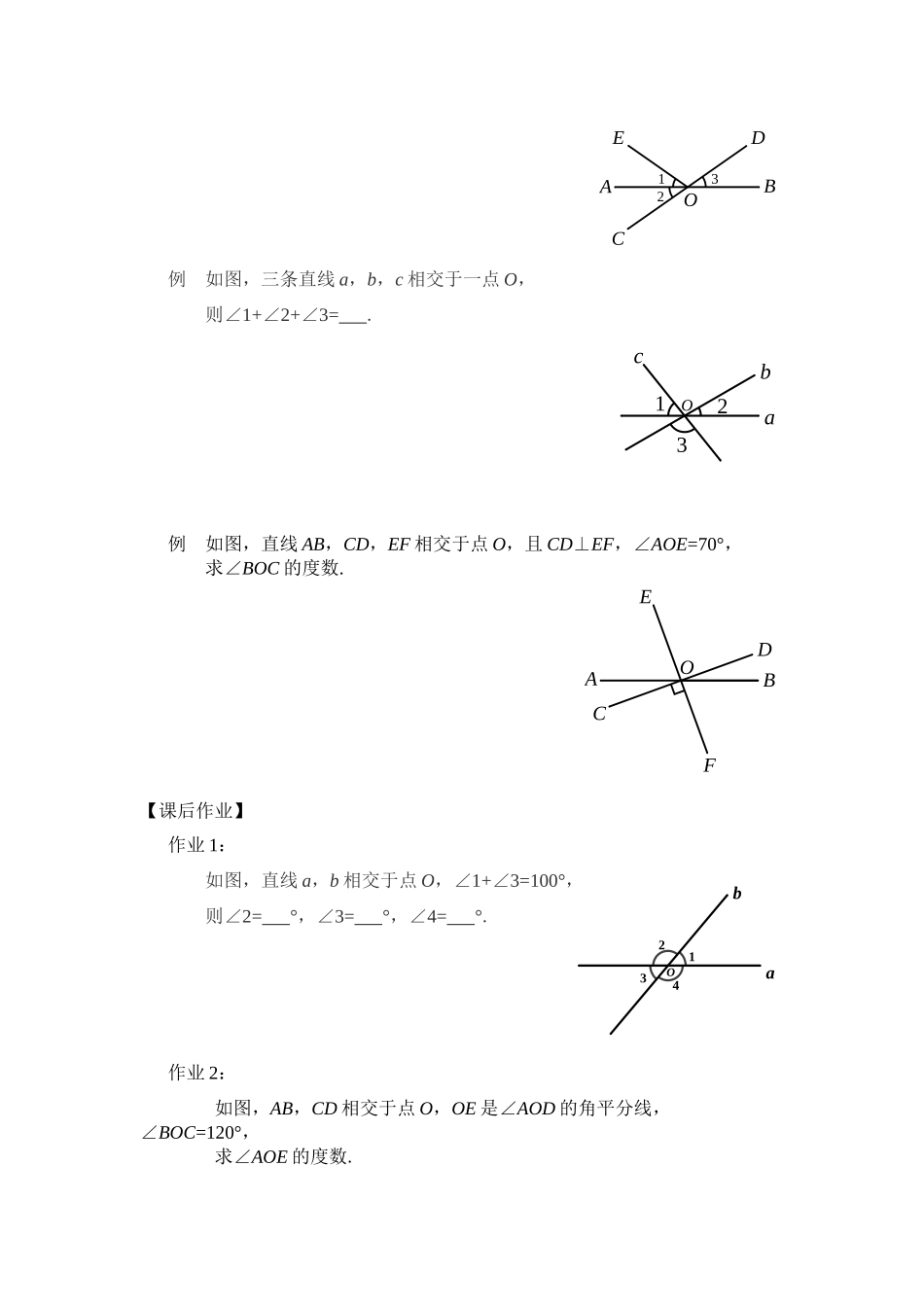
《邻补角与对顶角》学习任务单【学习目标】本节课的主要内容是结合两条直线相交的一般情况中,所形成的角的特殊位置关系,学习邻补角与对顶角的定义,探索并掌握“对顶角相等”的性质,经历几何直观的“简单说理”到几何论证的“简单推理”;培养学生的几何直观和推理能力;课堂中将通过四道例题来帮助学生完成以上的学习任务.【课上任务】1.请同学们在笔记本上画出:两条直线AB和CD相交于点O.2.如图,直线AB和CD相交于点O,图中四个角两两组合共有几对角?如何分类?4321OCDAB3.请同学们观察,第一类中的每对角,从角的构成要素上看,有什么共同特征呢?4.什么叫邻补角?5.由∠1与∠2的位置关系,你能够说一说它们的数量关系吗?6.辨析“邻补角”与“补角”,弄清二者的区别与联系.7.你能类比邻补角定义的形成过程,探究第二类角吗?依然从角的构成要素上看,第二类角有什么共同特征呢?8.什么叫对顶角?9.练习:判断下列各图中,∠1和∠2是不是对顶角?211212122110.大家猜一猜这两对对顶角具有怎样的数量关系?11.“对顶角相等”这个命题的题设和结论分别是什么?12.把“对顶角相等”改写成“如果……,那么……”的形式.13.根据命题的题设和结论,写出已知和求证.已知:求证:4321OCDAB14.对顶角的性质是什么?请跟随视频讲解,完成例题.例如图,直线a,b相交于点O,∠1=40°,求∠2,∠3,∠4的度数.ab1234O变式如图,直线a,b相交于点O,∠1∶∠2=2∶7,求∠2,∠3,∠4的度数.ab1234O例如图,AB,CD相交于点O,OA平分∠EOC,∠1=35°,求∠3的度数.123OEACDB例如图,三条直线a,b,c相交于一点O,则∠1+∠2+∠3=.acb321O例如图,直线AB,CD,EF相交于点O,且CD⊥EF,∠AOE=70°,求∠BOC的度数.FEABOCD【课后作业】作业1:如图,直线a,b相交于点O,∠1+∠3=100°,则∠2=°,∠3=°,∠4=°.作业2:如图,AB,CD相交于点O,OE是∠AOD的角平分线,∠BOC=120°,求∠AOE的度数.ab4321OABCDOE【课后作业参考答案】作业1参考答案:2=130°∠,∠3=50°,∠4=130°.作业2参考答案:解:∵直线AB和CD相交于O点(已知),∴∠AOD=∠BOC(对顶角相等).∵∠BOC=120°(已知),∴∠AOD=120°(等量代换).∵OE是∠AOD的角平分线(已知),∴∠AOE=12∠AOD=60°(角平分线的定义).