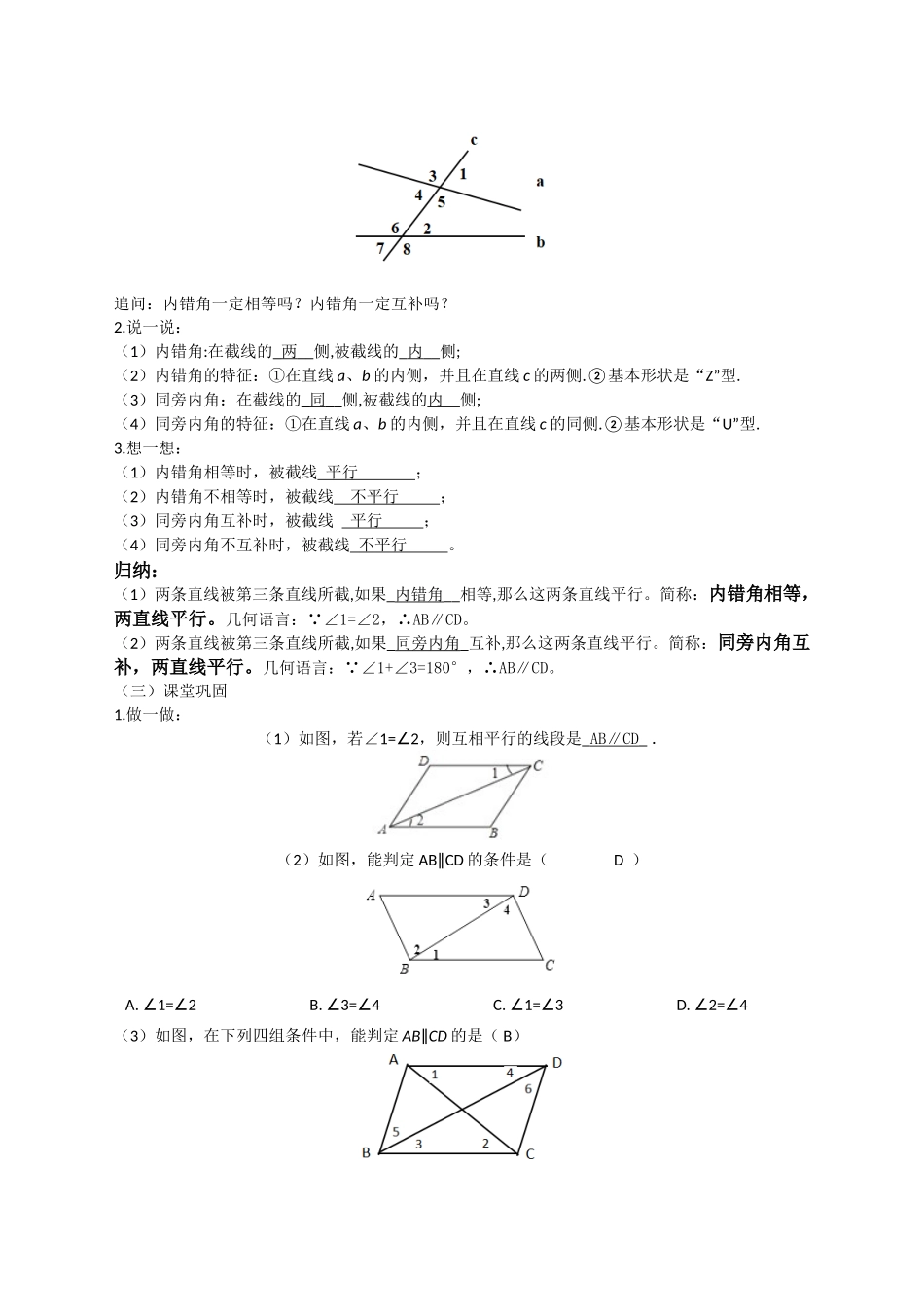
7.1探索直线平行的条件(2)一、教学目标1.知识与技能目标:(1)熟练识别内错角和同旁内角,并能将同位角、内错角及同旁内角熟练识别;(2)经历共同探究的过程,掌握直线平行的条件“内错角相等,两直线平行”、“同旁内角互补,两直线平行”,并能运用条件解决相关问题;2.过程与方法目标:通过推理、演变、猜测、交流等活动过程,进一步发展空间感知能力及推理归纳能力,提高逻辑推理能力及表达能力;3.情感态度与价值观目标:通过探究的过程,体会数学之间的联系与区别,激发学生对学习数学的兴趣。二、教学重难点1.教学重点:(1)熟练识别内错角和同旁内角;(2)理解直线平行的条件---“内错角相等,两直线平行”、“同旁内角互补,两直线平行”,并能运用条件解决实际问题。2.教学难点:灵活运用直线平行的条件,并能根据题意选择最恰当的方法。三、教学过程(一)课堂导入测一测:如图,线段CD、EF分别被线段AB所截,已知∠2=3∠,∠3+4=180°∠,请使用上节课所学的知识证明线段CD与线段EF平行。你能找到几种方法?方法一: ∠1=2∠(对顶角相等),∠2=3∠,(已知)1=3∴∠∠(等量代换)CDEF∴∥方法二: ∠3+4=180°∠(已知)3=180°∴∠-∠41+4=180° ∠∠(邻补角的性质)1=180°∴∠-∠41=3∴∠∠(等量代换)CDEF∴∥(二)预习交流1.找一找,上图中,你能找到几对内错角、几对同旁内角?下图呢?追问:内错角一定相等吗?内错角一定互补吗?2.说一说:(1)内错角:在截线的_两__侧,被截线的_内__侧;(2)内错角的特征:①在直线a、b的内侧,并且在直线c的两侧.②基本形状是“Z”型.(3)同旁内角:在截线的_同__侧,被截线的内侧;(4)同旁内角的特征:①在直线a、b的内侧,并且在直线c的同侧.②基本形状是“U”型.3.想一想:(1)内错角相等时,被截线平行;(2)内错角不相等时,被截线不平行;(3)同旁内角互补时,被截线平行;(4)同旁内角不互补时,被截线不平行。归纳:(1)两条直线被第三条直线所截,如果_内错角__相等,那么这两条直线平行。简称:内错角相等,两直线平行。几何语言: ∠1=∠2,∴AB∥CD。(2)两条直线被第三条直线所截,如果_同旁内角_互补,那么这两条直线平行。简称:同旁内角互补,两直线平行。几何语言: ∠1+∠3=180°,∴AB∥CD。(三)课堂巩固1.做一做:(1)如图,若∠1=2∠,则互相平行的线段是_AB∥CD_.(2)如图,能判定ABCD∥的条件是(D)A.1=2∠∠B.3=4∠∠C.1=3∠∠D.2=4∠∠...