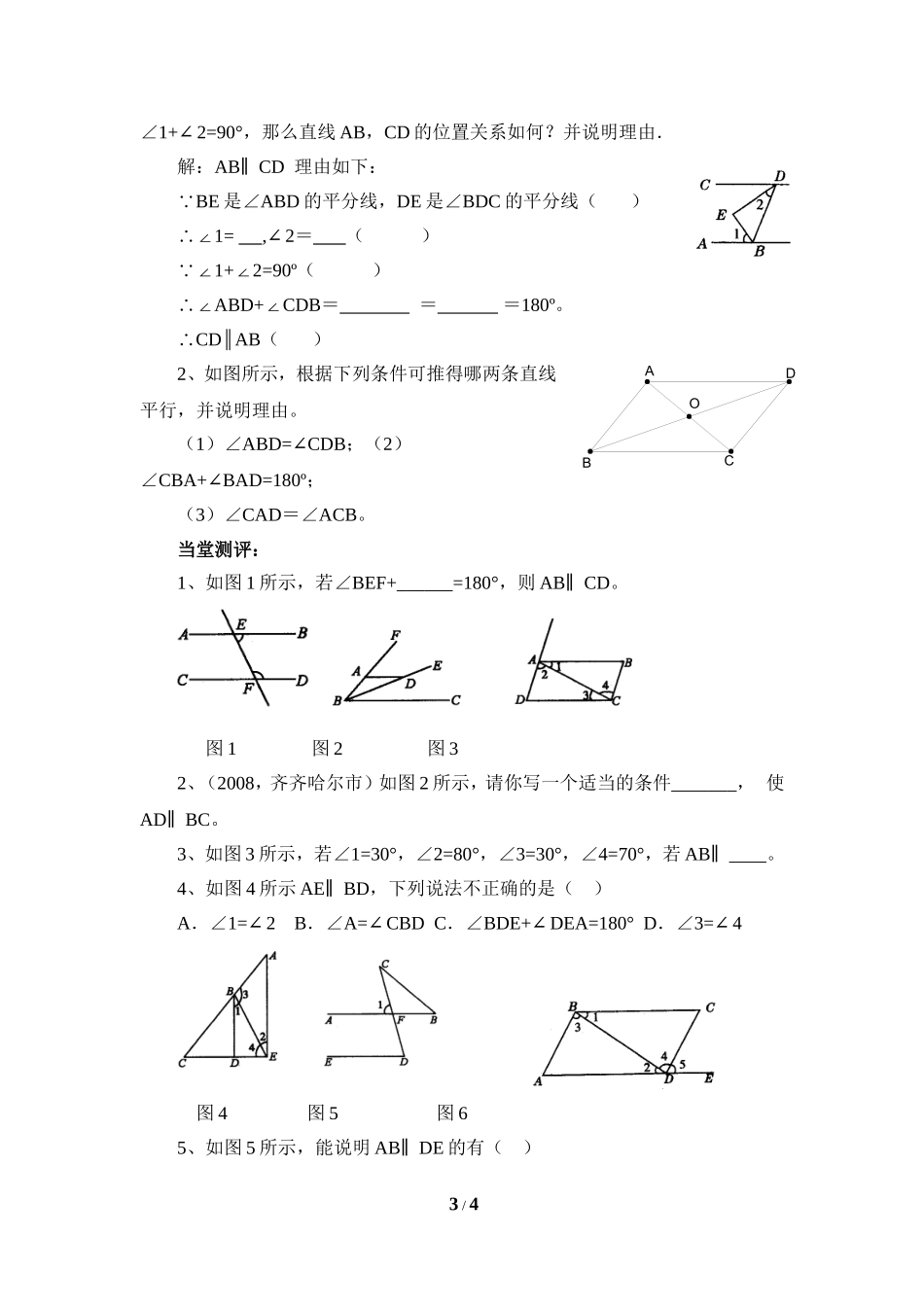
7.2探索直线平行的条件(2)一、学习目标:1、经历观察、操作、想象、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。2、经历探索直线平行的条件的过程,掌握直线平行的条件,并能解决一些问题。3、会用三角尺过已知直线外一点画这条直线的平行线。二、学习重点:弄清内错角和同旁内角的意义,会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。三、学习难点:会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”。四、学习设计(一)预习准备(1)预习书73-74页(2)回顾:①什么是同位角?什么是内错角?什么是同旁内角?②同位角相等,两直线平行。(3)预习作业:如图所示:1)如果1D,那么∥理由是2)如果1B,那么∥理由是3)如果0180AB,那么∥理由是4)如果0180AD,那么∥理由是(二)新课学习:平行判定2:两条直线被第三条直线所截,如果内错角,那么这两直线。简称:如图,可表述为: ()∴()1/4EDCBA12BDCA1平行判定3:两条直线被第三条直线所截,如果同旁内角,那么这两直线。简称:如图,可表述为: ()∴()例1、如右图, ∠1=∠2∴∥, ∠2=∴∥,(同位角相等,两直线平行) ∠3+∠4=180°∴∥,∴AC∥FG,变式训练:如图所示,AB⊥BC于点B,BC⊥CD于点C,∠1=∠2,那么EB∥CF吗?为什么?例2、如图,已知0040,1140B,那么AB∥CD成立吗?请说明理由。变式训练:如图所示,若∠1+∠2=180°,∠1=∠3,EF与GH平行吗?解:为∠1+∠2=180°()所以AB_______∥()又因为∠1=3∠()所以∠2+________=180°∠()所以EFGH∥()拓展:1、如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且2/4ABCDEFG1234DCBA112BDCA∠1+2=90°∠,那么直线AB,CD的位置关系如何?并说明理由.解:ABCD∥理由如下:BE 是∠ABD的平分线,DE是∠BDC的平分线()1=∴∠,2∠=()1+2=90º ∠∠()ABD+CDB∴∠∠===180º。CDAB∴∥()2、如图所示,根据下列条件可推得哪两条直线平行,并说明理由。(1)∠ABD=CDB∠;(2)∠CBA+BAD=180º∠;(3)∠CAD=∠ACB。当堂测评:1、如图1所示,若∠BEF+______=180°,则ABCD∥。图1图2图32、(2008,齐齐哈尔市)如图2所示,请你写一个适当的条件_______,使ADBC∥。3、如图3所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB____∥。4、如图4所示AEBD∥,下列说法不正确的是()A.∠1=2B∠....